Course Outline

list High School / Advanced Statistics and Data Science I (ABC)

Book
  • High School / Advanced Statistics and Data Science I (ABC)
  • High School / Statistics and Data Science I (AB)
  • High School / Statistics and Data Science II (XCD)
  • High School / Algebra + Data Science (G)
  • College / Introductory Statistics with R (ABC)
  • College / Advanced Statistics with R (ABCD)
  • College / Accelerated Statistics with R (XCD)
  • CKHub: Jupyter made easy

12.11 Confidence Interval for the Slope of a Regression Line

Let’s go back to the regression model we fit using total Check to predict Tip. We can specify this model of the DGP like this:

\[Y_i=\beta_0+\beta_{1}X_i+\epsilon_i\]

Here is the output for the best-fitting Check model using lm().

Call:
lm(formula = Tip ~ Check, data = TipExperiment)

Coefficients:
(Intercept)        Check
   18.74805      0.05074

Use the code window below to find the confidence interval for the slope of this regression line.

require(coursekata) # Simulate Check set.seed(22) x <- round(rnorm(1000, mean=15, sd=10), digits=1) y <- x[x > 5 & x < 30] TipPct <- sample(y, 44) TipExperiment$Check <- (TipExperiment$Tip / TipPct) * 100 # we’ve created the Check model for you Check_model <- lm(Tip ~ Check, data = TipExperiment) # find the confidence interval around the slope # we’ve created the Check model for you Check_model <- lm(Tip ~ Check, data = TipExperiment) # find the confidence interval around the slope confint(Check_model) ex() %>% check_function("confint") %>% check_result() %>% check_equal()
                 2.5 %      97.5 %
(Intercept) 12.76280568 24.73328496
Check        0.02716385  0.07431286

The \(\beta_1\) represents the increment that is added to the predicted tip in the DGP for every additional dollar spent on the total check. The confidence interval of \(\beta_1\) represents the range of \(\beta_1\)s that would be likely to produce the sample \(b_1\). About 3 cents is the lowest \(\beta_1\) that would be likely to produce the sample \(b_1\) and 7 cents is the highest.

Now that we have tried confint(), try using the resample() function to bootstrap the 95% confidence interval for the slope of the regression line. See how your bootstrapped confidence interval compares to the results obtained by using confint().

require(coursekata) # Simulate Check set.seed(22) x <- round(rnorm(1000, mean=15, sd=10), digits=1) y <- x[x > 5 & x < 30] TipPct <- sample(y, 44) TipExperiment$Check <- (TipExperiment$Tip / TipPct) * 100 # make a bootstrapped sampling distribution sdob1_boot <- # we’ve added some code to visualize this distribution in a histogram gf_histogram(~ b1, data = sdob1_boot, fill = ~middle(b1, .95), bins = 100) # make a bootstrapped sampling distribution sdob1_boot <- do(1000) * b1(Tip ~ Check, data = resample(TipExperiment)) # we’ve added some code to visualize this distribution in a histogram gf_histogram(~ b1, data = sdob1_boot, fill = ~middle(b1, .95), bins = 100) ex() %>% check_object("sdob1_boot") %>% check_equal()

Here is a histogram of the bootstrapped sampling distribution we created. Yours will be a little different, of course, because it is random.

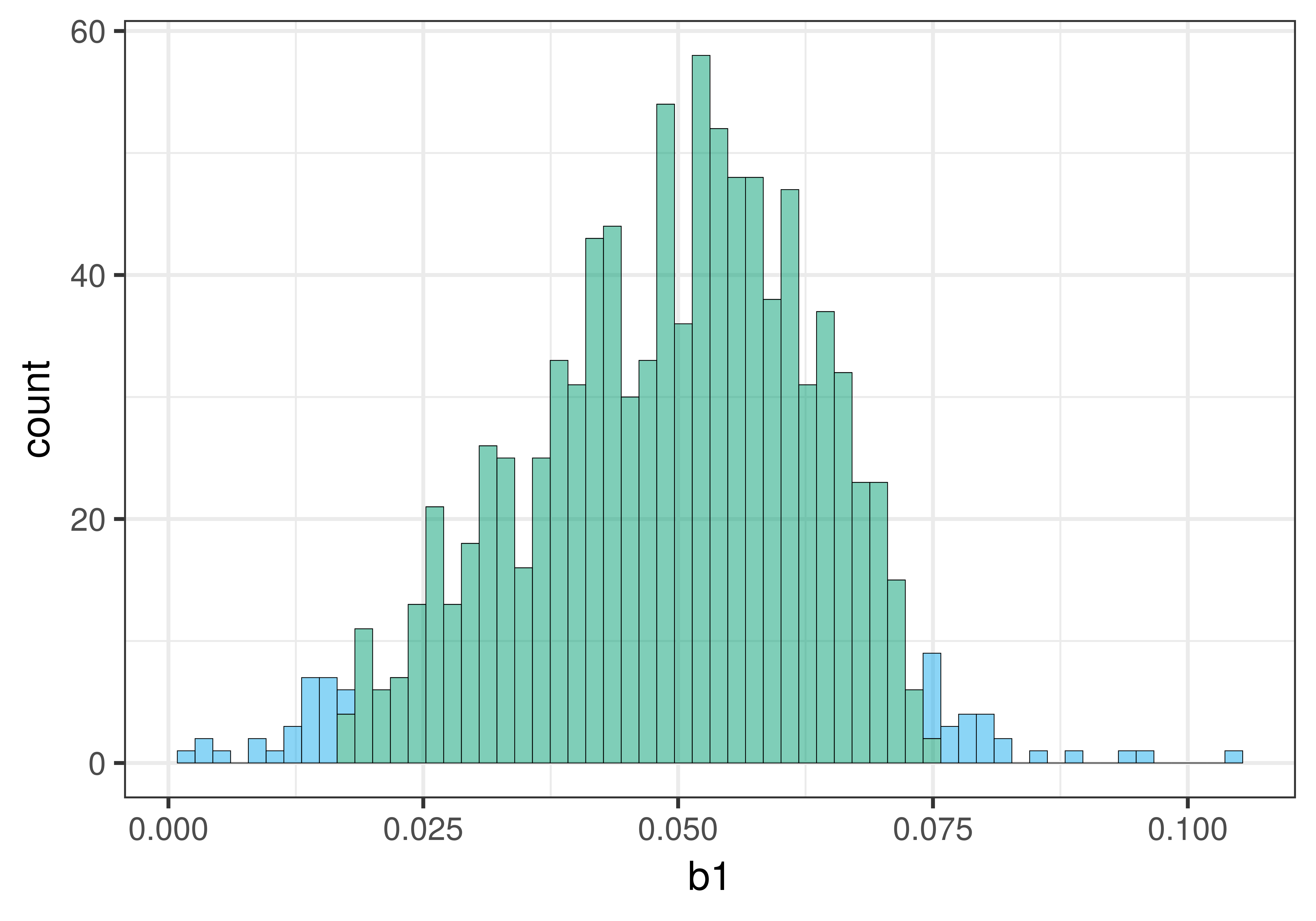
A histogram of the sampling distribution of b1. It is normal in shape, centered near 0.050, and ranges from about zero to 0.10. The tails of the distribution are shaded in blue, and the middle 95 percent of b1s are shaded in green. The blue of the lower tail extends from about zero to about 0.013, and the blue of the upper tail extends from about 0.075 to about 1.00. The range along the y-axis extends from zero to 60.

The center of the bootstrapped sampling distribution is approximately the same as the sample \(b_1\) of .05. This is what we would expect because bootstrapping assumes that the sample is representative of the DGP.

As explained previously, we can use the .025 cutoffs that separate the unlikely tails from the likely middle of the sampling distribution as a handy way to find the lower and upper bound of the 95% confidence interval. We can eyeball these cutoffs by looking at the histogram, or we can calculate them by arranging the bootstrapped sampling distribution to find the actual 26th and 975th b1s.

require(coursekata) # Simulate Check set.seed(22) x <- round(rnorm(1000, mean=15, sd=10), digits=1) y <- x[x > 5 & x < 30] TipPct <- sample(y, 44) TipExperiment$Check <- (TipExperiment$Tip / TipPct) * 100 # we have made a bootstrapped sampling distribution sdob1_boot <- do(1000) * b1(Tip ~ Check, data = resample(TipExperiment)) # modify the code below to arrange the sampling distribution in order by b1 sdob1_boot <- arrange() # find the 26th and 975th b1 sdob1_boot$b1[ ] sdob1_boot$b1[ ] # we have made a bootstrapped sampling distribution sdob1_boot <- do(1000) * b1(Tip ~ Check, data = resample(TipExperiment)) # modify the code below to arrange the sampling distribution in order by b1 sdob1_boot <- arrange(sdob1_boot, b1) # find the 26th and 975th b1 sdob1_boot$b1[26] sdob1_boot$b1[975] ex() %>% { check_output_expr(., "sdob1_boot$b1[26]") check_output_expr(., "sdob1_boot$b1[975]") }
0.0172834762542693
0.0757609233182571

To find the confidence interval, we sorted the randomly generated \(b_1\)s from lowest to highest, and then used the 26th and 975th \(b_1\)s as the lower and upper bounds of the confidence interval. Your results will be a little different from ours because resampling is random. We got a bootstrapped confidence interval of .02 to .07, which is close to what we got from confint() (.027 and .074).

The bootstrapped sampling distribution of slopes in this case is not exactly symmetrical; it is a bit skewed to the right. For this reason, the center of the confidence interval will not be exactly at the sample \(b_1\). This is in contrast to the mathematical approach that assumes that the sample \(b_1\) is exactly in the middle of a perfectly symmetrical t-distribution. This difference does not mean that bootstrapping is less accurate. It might be that there is something about the distributions of Check and Tip that results in this asymmetry.

The important thing we want to focus on for now is that all of these methods result in approximately the same results. These similarities show us what confidence intervals mean and what they can tell us. Later, in more advanced courses, you can take up the question of why the results differ across methods when they do.

Responses

Responses
close