10.4 What Counts as Unlikely?

All of this, however, begs the question of how extreme a sample \(b_1\) would need to be in order for us to reject the empty model. What is unlikely to one person might not seem so unlikely to another person. It would help to have some sort of agreed upon standard of “what counts as unlikely” before we actually bring in our real sample statistic. The definition of “unlikely” depends on what you are trying to do with your statistical model and what your community of practice agrees on.

One common standard used in the social sciences is that a sample counts as unlikely if there is less than a .05 chance of generating one that extreme (in either the negative or positive direction) from a particular DGP. We notate this numerical definition of “unlikely” with the Greek letter \(\alpha\) (pronounced “alpha”). A scientist might describe this criterion by writing or saying that they “set alpha equal to .05”. If they wanted to use a stricter definition of unlikely, they might say “alpha equals .001,” indicating that a sample would have to be really unlikely for us to reject the empty model of the DGP.

Let’s try setting an alpha level of .05 to the sampling distribution of \(b_1\)s we generated from random shuffles of the tipping study data. If you take the 1000 \(b_1\)s and line them up in order, the .025 lowest values and the .025 highest values would be the most extreme 5% of values and therefore the most unlikely values to be randomly generated.

In a two-tailed test, we will reject the empty model of the DGP if the sample is not in the middle .95 of randomly generated \(b_1\)s. We can use a function called middle() to fill the middle .95 of \(b_1\)s in a different color.

gf_histogram(~b1, data = sdob1, fill = ~middle(b1, .95))

The fill= part tells R that we want the bars of the histogram to be filled with particular colors. The ~ tells R that the fill color should be conditioned on whether the \(b_1\) being graphed falls in the middle .95 of the distribution or not.

Here’s what the histogram of the sampling distribution looks like when you add fill = ~middle(b1, .95) to gf_histogram().

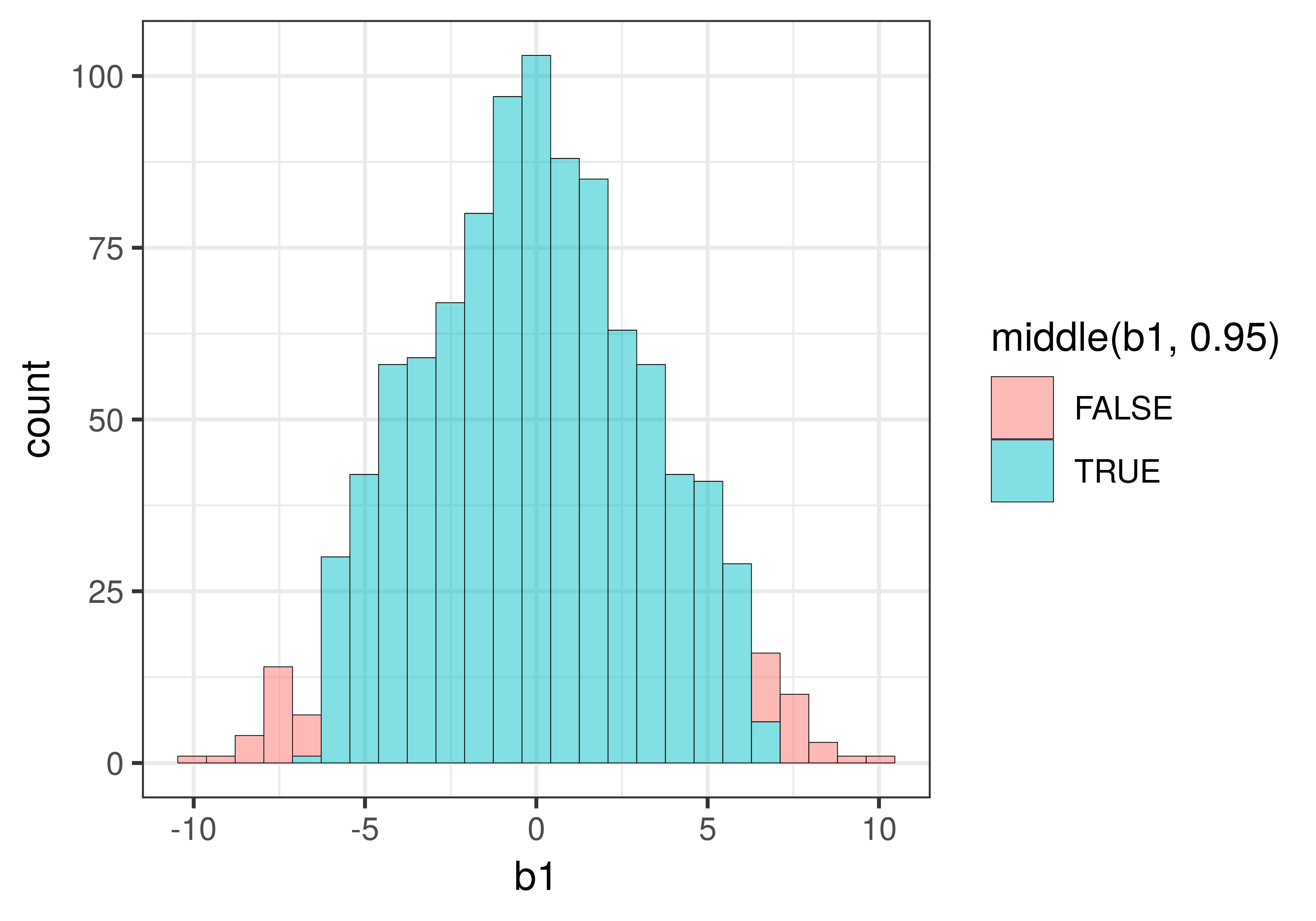
​​ You might be wondering why some of the bars of the histogram include both red and blue. This is because the data in a histogram is grouped into bins. The value 6.59, for example, is grouped into the same bin as the value 6.68, but while 6.59 falls within the middle .95 (thus colored blue), 6.68 falls just outside the .025 cutoff for the upper tail (and thus is colored red).

If you would like to see a more sharp delineation, you could try making your bins smaller, or to put it another way, making more bins. Doing so would increase the chances of having just one color in each bin.

We re-made the histogram, but this time added the argument bins = 100 to the code (the default number of bins is 30). We also added show.legend = FALSE to get rid of the legend, and thus provide more space for the plot.

gf_histogram(~b1, data = sdob1, fill = ~middle(b1, .95), bins = 100, show.legend = FALSE)

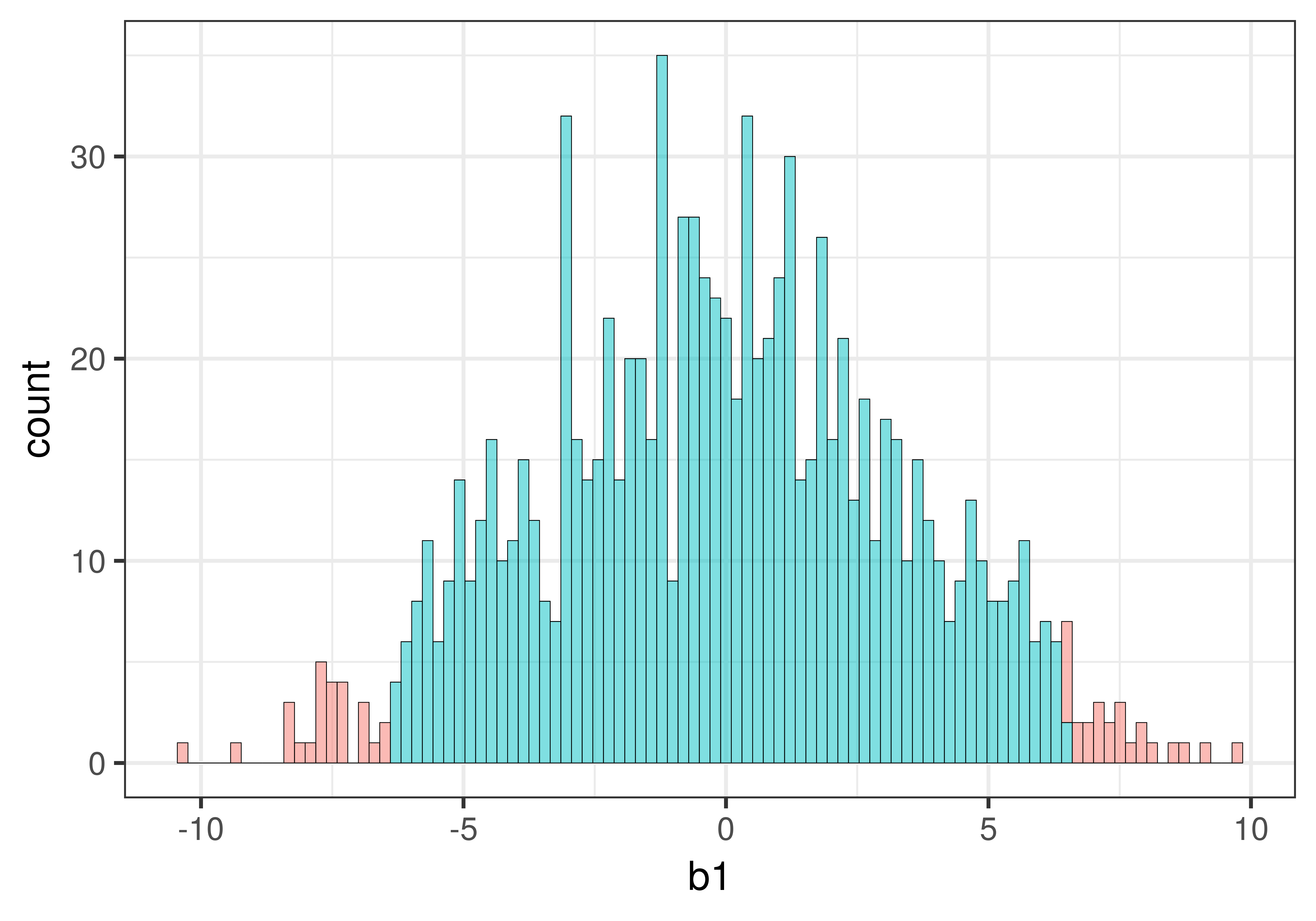
​​ Increasing the number of bins resulted in each bin being represented by only one color. But it also created some holes in the histogram, i.e., empty bins in which none of the sample \(b_1\)s fell. This is not a problem, it’s just a natural consequence of increasing the number of bins.

Remember, this histogram represents a sampling distribution. All these \(b_1\)s were the result of 1000 random shuffles of our data. None of these is the \(b_1\) calculated from the actual tipping experiment data. All of these \(b_1\)s were created by a DGP where the empty model is true.

In the actual experiment of course, we only have one sample. If our actual sample \(b_1\) falls in the region of the sampling distribution colored red (based on the alpha we set), we will doubt that it was generated by the DGP that assumes \(\beta_1=0\). In this case, based on our alpha criterion, we would reject the empty model. This could be the right decision…

But it might be the wrong decision. If the empty model is true, .05 of the \(b_1\)s that could result from different randomizations of tables to conditions would be extreme enough to lead us to reject the empty model. If we rejected the empty model when it is, in fact, true, we would be making a Type I error. By setting the alpha at .05, we are saying that we are okay with having a 5% Type I error rate.

What is the Opposite of Unlikely?

We’re going to be interested in whether our sample \(b_1\) falls in the .05 unlikely tails. But what if it doesn’t fall in the tails but instead in the middle part of the sampling distribution? Should we then call it “likely”?

To be precise, if the sample falls in the middle .95 of the sampling distribution, it means that the sample is not unlikely. But saying that it is likely is a little bit sloppy, and possibly misleading.

In statistics, even if an event has a probability of .06, we will say it is not unlikely because our definition of unlikely is .05 or lower. But a regular person would not call something with a likelihood of .06 “likely”.

It gets tiring to say not unlikely all the time, and sometimes sentences read a little bit easier if we just say likely. Just remember that when we say likely we usually mean not unlikely. But this is not what normal people mean by the word likely.