6.11 The Empirical Rule

The cool thing about normal distributions is that they all basically follow this pattern. In the smooth perfect version of the normal distribution (i.e., the theoretical probability distribution), Zone 1 covers about .68, Zone 2 covers .95, and Zone 3 covers .997. This .68-.95-.997 pattern is called the empirical rule.

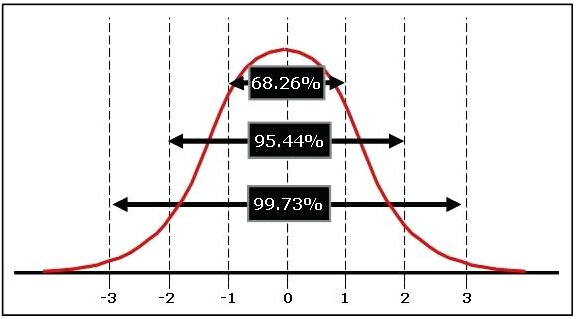
The empirical rule tells us:

• Approximately 68 percent of the scores in a normal distribution are within one standard deviation, plus or minus, of the mean.

• Approximately 95 percent of the scores are within two standard deviations.

• Approximately 99.7 percent of scores are within three standard deviations of the mean (in other words, almost all of them).

The smooth normal distribution is something that is so perfect that it doesn’t really exist. It’s a mathematical object, kind of like how there are straight lines in the world, but a mathematical straight line is this perfect thing that has no mass, no jitter, and goes on forever. In the same way, a mathematical normal distribution is perfect with no mass, no jitter, and it goes on forever.

The tails of the normal distribution never quite hit 0, they just go on forever and ever. This is why the normal distribution is sometimes called asymptotic. This feature is important because it allows us to predict the very tiny probabilities of very unlikely events such as a person with a thumb length of 1,000 mm.

You probably have never even heard of a thumb so long. But, if we assume the normal probability distribution, we could quantify exactly how low the probability would be of finding such a rare event.

You can try making up a standard deviation for your own game (we’ll call it Zargle) and simply run the code. It will show you the histograms and proportions for the three zones. Try some different standard deviations to try and break the empirical rule.

This is what we would get for the Zargle distribution if the standard deviation was set for 3,500.

       zone Bargle Kargle  Zargle
1         1 0.6844 0.6822 0.67965
2         2 0.9518 0.9487 0.95360
3         3 0.9982 0.9972 0.99680
4 outside 3 0.0018 0.0028 0.00320

The empirical rule can be very useful when trying to make a quick interpretation of a specific score. If a friend has a baby and tells you it was 54 cm long, how would you interpret that measurement? As an experienced statistician, you should ask: what is the mean, and what is the standard deviation, of the distribution of baby length at birth?

As it turns out, the mean baby length is roughly 50 cm, and the standard deviation is 2 cm. Using the empirical rule, you would say, “Wow! Your baby is like two standard deviations above the mean! That’s a huge baby! Only .05 of babies are longer than 54 cm (the mean plus two standard deviations). You’ve got yourself a big one!”

Actually, you’d be slightly wrong. (Sorry, I know we set you up!) According to the empirical rule, .95 scores in a normal distribution are within plus or minus two standard deviations from the mean. It follows from this that .05 of the scores are more extreme than this, or outside plus or minus two standard deviations.

But note, in the figure, that if .05 of the scores are outside plus or minus two standard deviations, half of those would be expected to be more than two standard deviations above the mean, and half less than two standard deviations below the mean.

So, only .025 of scores would be higher than two standard deviations above the mean. That baby is even more impressive than we thought! He or she is longer than 97.5% of all babies!

What Counts as Unlikely?

We have seen how modeling the error distribution (in the case of the empty model, the distribution of scores around the mean) can help us to calculate probabilities and make predictions. The problem with a probability, though, is that it’s just a number. It doesn’t tell us what to do. We still have to think about it even after all our fancy R code calculations.

For example, if we wanted to use a model of finger lengths to design stretchy one-size-fits-all gloves, how big should we make the gloves? After all, even though very long thumbs are unlikely, they are still possible. But if we make these gloves too big, then we’ll alienate short-fingered folks.

What would be the right glove size? To answer questions like this, we have to figure out what are the most likely lengths of people’s fingers, and that means we need to make a judgment call about what “likely” and “unlikely” mean. We might be able to agree on the best way to estimate a probability, but people will differ on what counts as “unlikely.”

For example, someone who is very risky might look at a .01 probability and say, “Hey! At least it is still possible.” But someone who likes being very certain might say, “Even .40 is unlikely because it’s less likely than a coin toss!” So in being part of a statistics community, it’s helpful to have an agreement about what counts as unlikely.

Statisticians, as a community, have decided to count .05 and lower probabilities as unlikely. So in the case of a DGP that produces a fairly normal population, we would count scores that are outside of Zone 2 (+/- two standard deviations from the mean) as unlikely scores, and the scores within Zone 2 as likely. Note that this decision doesn’t result from a calculation. Human statisticians just sort of agree—yeah, .05 is a pretty low likelihood.