High School / Advanced Statistics and Data Science I (ABC)

Book

8 – Digging Deeper into Group Models

8.1 Extending to a Three-Group Model

You have now learned how to specify a model with a single categorical explanatory variable consisting of two groups. It’s actually pretty simple to extend this idea to a categorical variable with three groups.

First, a New Two-Group Model

Let’s use a new explanatory variable to explain variation in thumb length: Height. Height, in our data set, is a quantitative variable measured in inches. But we can make a new variable that turns Height into a categorical variable with two categories: short and tall.

We can do this using the ntile() function in R. The code below will cut the sample up into two equal-sized groups based on Height and save the result into a new variable called Height2Group.

Fingers$Height2Group <- ntile(Fingers$Height, 2)
head(select(Fingers, Thumb, Height, Height2Group), 10)

We used head() and select() to look at the first 10 rows of the relevant variables – Thumb, Height, and Height2Group:

   Thumb Height Height2Group
1  66.00   70.5            2
2  64.00   64.8            1
3  56.00   64.0            1
4  58.42   70.0            2
5  74.00   68.0            2
6  60.00   68.0            2
7  70.00   69.0            2
8  55.00   65.7            2
9  60.00   62.5            1
10 52.00   63.4            1

In the code window below, use the factor() function to add labels to Height2Group so that the 1s are labeled as short and the 2s are labeled as tall.

require(coursekata)

Fingers <- Fingers %>% mutate(
   Height2Group = ntile(Height, 2)
)

# this creates Height2Group, a numeric variable
Fingers$Height2Group <- ntile(Fingers$Height, 2)

# this is how we used factor() before:
Fingers$Sex <- factor(Fingers$Sex, levels = c(1,2), labels = c("female", "male"))

# modify this line so that 1s are labeled as "short" and 2s are labeled as "tall"
Fingers$Height2Group <- factor()

# this prints out 10 rows of Fingers for the selected columns
head(select(Fingers, Thumb, Height, Height2Group), 10)

Fingers$Height2Group <- factor(Fingers$Height2Group, levels = 1:2, labels = c("short", "tall"))

head(select(Fingers, Thumb, Height, Height2Group), 10)

ex() %>% {
   check_object(., "Fingers") %>% check_column("Height2Group") %>% check_equal()
   check_output_expr(., "head(select(Fingers, Thumb, Height, Height2Group), 10)")
}

CK Code: B4_Code_Extending_01

   Thumb Height Height2Group
1  66.00   70.5         tall
2  64.00   64.8        short
3  56.00   64.0        short
4  58.42   70.0         tall
5  74.00   68.0         tall
6  60.00   68.0         tall
7  70.00   69.0         tall
8  55.00   65.7         tall
9  60.00   62.5        short
10 52.00   63.4        short

Using the same approach we used for sex, we can write the model for Height2Group like this:

\[Thumb_i=b_0+b_1Height2Group_i+e_i\]

Go ahead and fit the Height2Group model, and print out the parameter estimates and ANOVA table for the model.

require(coursekata)

Fingers <- Fingers %>% mutate(
    Height2Group = factor(ntile(Height, 2), 1:2, c("short", "tall"))
)

# fit a model for Thumb ~ Height2Group
Height2Group_model <-

# this prints out the estimates
Height2Group_model

Height2Group_model <- lm(formula = Thumb ~ Height2Group, data = Fingers)
Height2Group_model

ex() %>% {
    check_function(., "lm") %>% check_arg("formula") %>% check_equal()
    check_object(., "Height2Group_model") %>% check_equal()
    check_output_expr(., "Height2Group_model")
}

CK Code: B4_Code_Extending_02

Call:
lm(formula = Thumb ~ Height2Group, data = Fingers)

Coefficients:
     (Intercept)  Height2Grouptall  
          57.818             4.601

Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height2Group

                               SS  df      MS      F    PRE     p
----- --------------- | --------- --- ------- ------ ------ -----
Model (error reduced) |   830.880   1 830.880 11.656 0.0699 .0008
Error (from model)    | 11049.331 155  71.286                    
----- --------------- | --------- --- ------- ------ ------ -----
Total (empty model)   | 11880.211 156  76.155

A Three-Group Model

Now let’s try this same approach with three height groups: short, medium, and tall.

Revise the code below to make a new variable called Height3Group that divides the sample into three categories based on Height, each with an equal number of students. Label the levels (1,2,3) as short, medium, and tall.

require(coursekata)

Fingers <- Fingers %>% mutate(
    Height2Group = factor(ntile(Height, 2), 1:2, c("short", "tall"))
)
Height2Group.model <- lm(Thumb ~ Height2Group, data = Fingers)

# modify these two lines of code to create 3 Height groups with the labels "short", "medium", and "tall"
# make sure you save to a new variable in Fingers called Height3Group
Fingers$Height2Group <- ntile(Fingers$Height, 2)
Fingers$Height2Group <- factor(Fingers$Height2Group, levels = c(1,2), labels = c("short", "tall"))

# this prints out 10 rows of Fingers for selected columns
head(select(Fingers, Thumb, Height, Height3Group), 10)

Fingers$Height3Group <- ntile(Fingers$Height, 3)
Fingers$Height3Group <- factor(Fingers$Height3Group, levels = c(1,2,3), labels = c("short", "medium", "tall"))

head(select(Fingers, Thumb, Height, Height3Group), 10)

ex() %>% {
    check_object(., "Fingers") %>% check_column("Height3Group") %>% check_equal()
    check_output_expr(., "head(select(Fingers, Thumb, Height, Height3Group),10)")
}

CK Code: B4_Code_Extending_03

   Thumb Height Height3Group
1  66.00   70.5         tall
2  64.00   64.8       medium
3  56.00   64.0        short
4  58.42   70.0         tall
5  74.00   68.0         tall
6  60.00   68.0         tall
7  70.00   69.0         tall
8  55.00   65.7       medium
9  60.00   62.5        short
10 52.00   63.4        short

Calculate and print out the group means of Thumb for the three height groups.

require(coursekata)

Fingers <- Fingers %>% mutate(
    Height2Group = factor(ntile(Height, 2), 1:2, c("short", "tall")),
    Height3Group = factor(ntile(Height, 3), 1:3, c("short", "medium", "tall"))
)
Height2Group.model <- lm(Thumb ~ Height2Group, data = Fingers)

# use favstats() to print the group means of Thumb length for the three height groups you created earlier
favstats()

favstats(Thumb ~ Height3Group, data = Fingers)

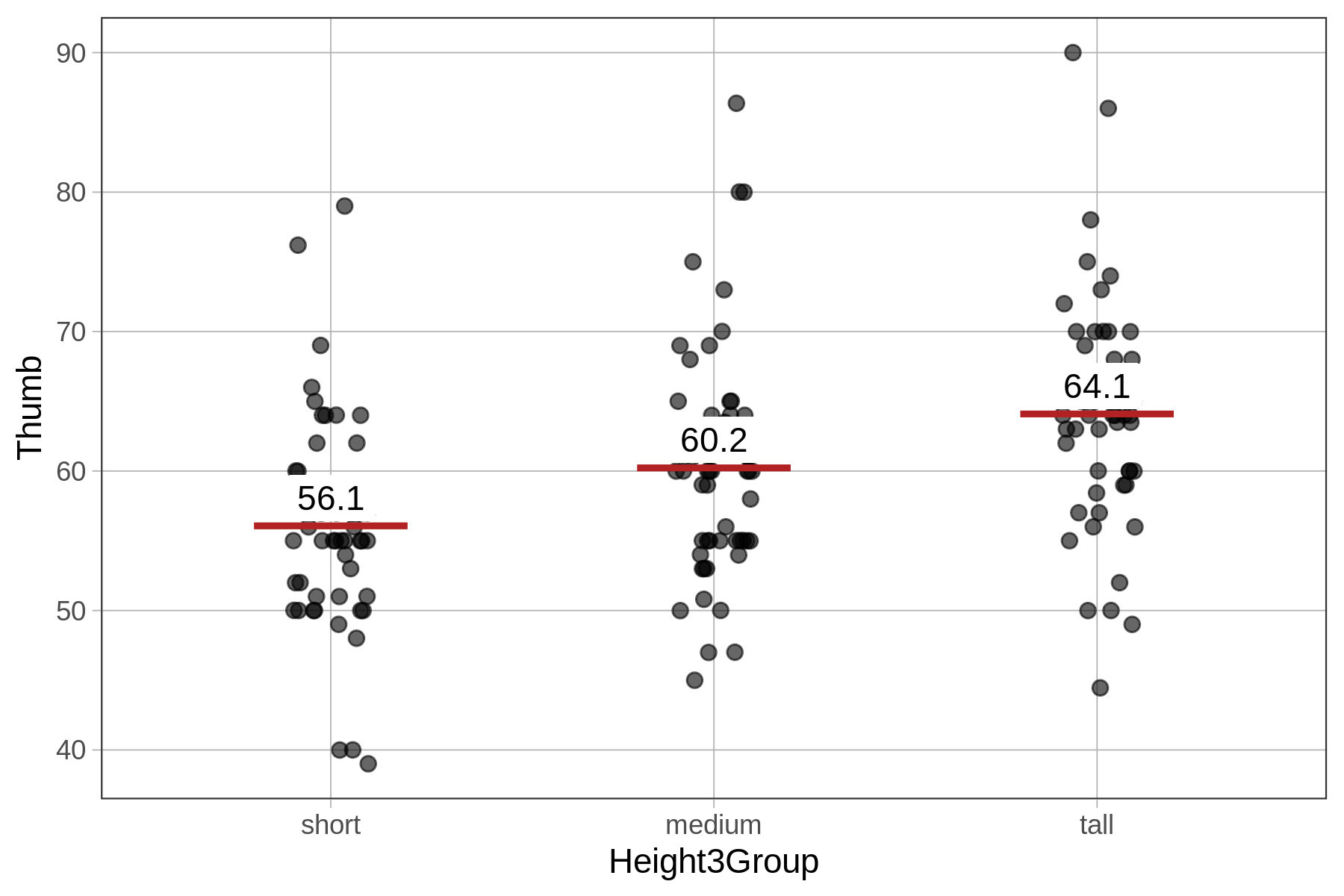
ex() %>% check_function("favstats") %>% check_result() %>% check_equal()

CK Code: B4_Code_Extending_04

  Height3Group   min    Q1 median    Q3   max     mean       sd  n missing
1        short 39.00 51.00     55 58.42 79.00 56.07113 7.499937 53       0
2       medium 45.00 55.00     60 64.00 86.36 60.22375 8.490406 52       0
3         tall 44.45 59.75     64 68.25 90.00 64.09365 8.388113 52       0

Here is a jitter plot that shows the distribution of thumb lengths for each of the three height groups and the mean of each group. On the next page, we’ll learn how to create a model of thumb length based on the three height groups.

NEED ALT TEXT

7.11 Chapter 7 Review Questions 8.2 Fitting and Interpreting the Three-Group Model

Course Outline

High School / Advanced Statistics and Data Science I (ABC)

8 – Digging Deeper into Group Models

8.1 Extending to a Three-Group Model

First, a New Two-Group Model

A Three-Group Model

Responses

list High School / Advanced Statistics and Data Science I (ABC)

8 – Digging Deeper into Group Models

8.1 Extending to a Three-Group Model

First, a New Two-Group Model

A Three-Group Model

High School / Advanced Statistics and Data Science I (ABC)