Course Outline

list High School / Statistics and Data Science II (XCD)

Book
  • College / Advanced Statistics and Data Science (ABCD)
  • College / Statistics and Data Science (ABC)
  • High School / Advanced Statistics and Data Science I (ABC)
  • High School / Statistics and Data Science I (AB)
  • High School / Statistics and Data Science II (XCD)

3.8 Interpreting the Parameter Estimates for a Regression Model

Previously, we used the lm() function to fit the HomeSizeK model of PriceK and saved it as HomeSizeK_model:

HomeSizeK_model` <- lm(PriceK ~ HomeSizeK, data = Ames)

We used this model to generate predictions, but now let’s look at the parameter estimates and see how to interpret them.

We’ve already saved the model as HomeSizeK_model. Print its contents out in the code block below.

library(coursekata) # saves the home size model HomeSizeK_model <- lm(PriceK ~ HomeSizeK, data = Ames) # print it out # saves the home size model HomeSizeK_model <- lm(PriceK ~ HomeSizeK, data = Ames) # print it out HomeSizeK_model # temporary SCT ex() %>% check_output_expr("HomeSizeK_model")
CK Code: x3_Code_Interpreting_01
Call:
lm(formula = PriceK ~ HomeSizeK, data = Ames)

Coefficients:
(Intercept)    HomeSizeK  
      24.68       106.60

The Intercept corresponds to \(b_{0}\) and the HomeSizeK coefficient corresponds to \(b_{1}\). We can write our fitted model as:

\[PriceK_{i}=24.68 + 106.60HomeSizeK_{i}+e_{i}\]

Or, equivalently, using GLM notation, it can be written:

\[Y_{i}=24.68 + 106.60X_{i}+e_{i}\]

\(b_0\), which equals 24.68, is the y-intercept. It’s the predicted \(Y_i\) (PriceK) when \(X_i\) (HomeSizeK) equals 0.

How Regression Models Make Predictions

Similar to our use of the Neighborhood model, we can use the HomeSizeK model to predict the price at which a new home will sell. This time, however, we will adjust the prediction based on home size instead of neighborhood.

Recall that price (and predicted price) are in $1000 dollar units. The \(b_0\) (24.68 or $24,680) represents the predicted price for a home with a size of 0. If we stretch out the x-axis to include 0, we would expect the regression line to cross the y-axis at 24.68. (Notice, however, that in the plot below that there are no actual homes of size 0, for obvious reasons!)

A scatterplot of PriceK by HomesizeK in the Ames data frame. It is overlaid with the regression line in red. An arrow points to the part of the regression line where the x-axis equals zero and has the caption: when HomeSizeK equals zero, predicted PriceK equals 24.68.

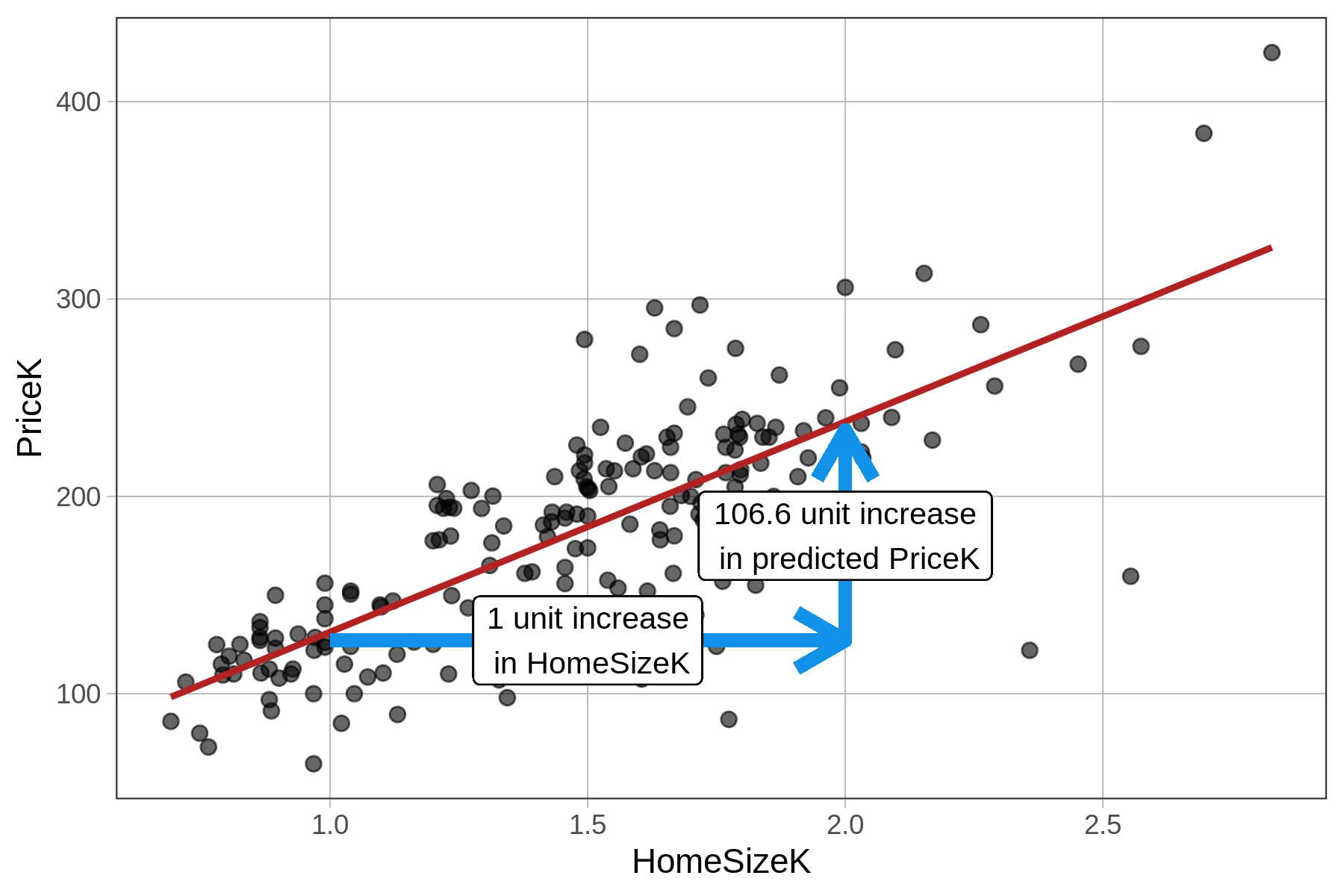
The \(b_1\) estimate (106.60) is the slope: for every 1 unit increase in HomeSizeK, our model predicts a 106.60 increase in PriceK. Because both of our variables represent units in thousands (HomeSizeK is thousands of square feet and PriceK is thousands of dollars), this means that homes with 1K more square feet are predicted by our model to have a $106.60K higher price tag (on average). Here’s a visual representation:

A scatter plot of PriceK by HomesizeK in the Ames data frame. It is overlaid with the regression line in red. An arrow starts from the point along the regression line where the x-axis equals one and horizontally points to the right to where the x-axis equals two. The caption for the arrow says: one unit increase in HomeSizeK. A second arrow points up from the nose of the horizontal arrow to the regression line with the caption: 106.6 unit increase in predicted PriceK.

The predicted price of a 2.41K square foot home (that is, 2,410 square feet) is $281.59K. This is the \(Y_i\) (PriceK) on the regression line when \(X_i\) (HomeSizeK) is 2.41, as visualized below:

A scatterplot of PriceK by HomesizeK in the Ames data frame. It is overlaid with the regression line in red. A dashed line extends from the x-axis where HomeSizeK equals 2.41 up to the regression line. That is the point along the line where the predicted PriceK equals 282.59

Comparing the Neighborhood Model and the HomeSizeK Model

Having now specified and fit two models, one a group model and the other a regression model, let’s just think for a bit on what the similarities and differences are between these models.

Symbol Group Mean Model
\({Price}_{i}=b_{0}+b_{1}{Neighborhood}_{i}+e_{i}\) 		Regression Model
\({Price}_{i}=b_{0}+b_{1}{HomeSize}_{i}+e_{i}\)
\(Y_i\) Price of home i Price of home i
\(b_0\) Predicted home price when \(Neighborhood_i = 0\))
(mean home price in College Creek) 		Predicted home price when \(HomeSize_i=0\)
(y-intercept for regression line)
\(b_1\) Adjustment to predicted price for a home in Old Town
(the mean difference between the two group means) 		Adjustment to predicted price for a one-unit increase in home size
(the slope of the regression line)
\(X_i\) Neighborhood of home i, coded as 0=not-Old Town, 1=Old Town Home size of home i in thousands of square feet
\(e_i\) Error for home i Error for home i


Responses

Responses
close