Chapter 3 - Modeling Relationships in Data

3.1 Explaining Variation

Having now spent some time with the empty model, you may be wondering, “What is the point of that model?” Statistics is supposed to help us explain variation and make better predictions of the outcome based on other variables. But the empty model doesn’t seem to make very good predictions. Yes, the mean is the point in the distribution that reduces the sum of squares to its lowest point. But surely that doesn’t count as an explanation of variation!

Indeed it does not. We started with the empty model but that’s not where we want to end up. We will use the empty model as a reference point to help us see if our more complex models that include explanatory variables are better. Note that even though we will refer to models in this chapter as “complex” – they are still relatively simple. We just mean that these models are more complex than the empty model.

Explaining Variation in Home Prices

Let’s start by reviewing what we mean by explaining variation. In the previous chapter, we looked at the distribution of home prices in Ames broken down by neighborhood in a jitter plot. We’ve added the empty model (the mean home price) for reference.

empty_model <- lm(PriceK ~ NULL, data = Ames)
 
gf_jitter(PriceK ~ Neighborhood, data = Ames, width = .1) %>%
gf_model(empty_model)

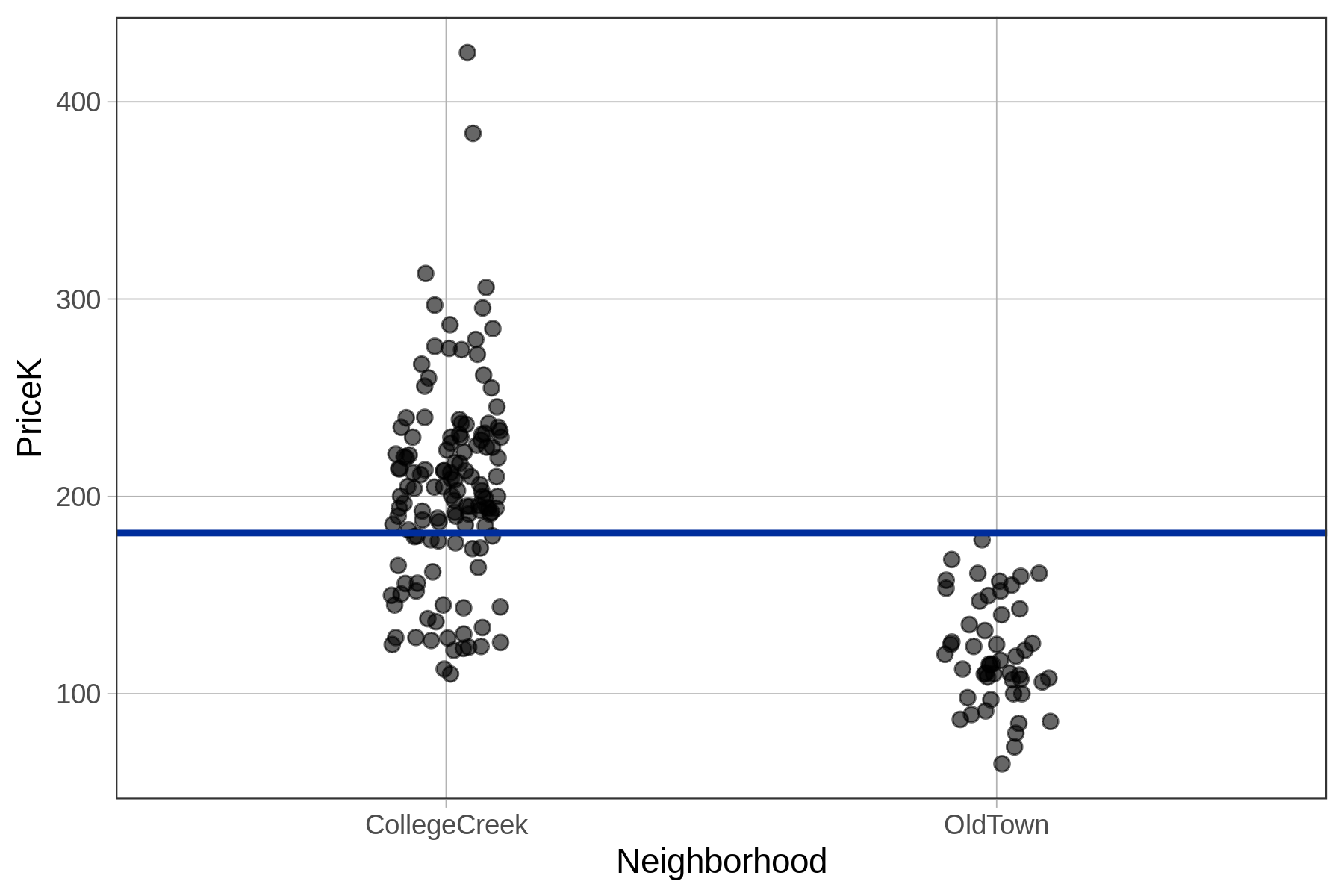
We can see from this graph that there appears to be a relationship in the data between neighborhood and home prices. Applying our informal definition of explain variation, it appears from the graph that if we know which neighborhood a home is in, we can make a better guess about its price.

We can express this relationship between Neighborhood and PriceK informally with a word equation:

PriceK = Neighborhood + Error

We will refer to this as the Neighborhood model of PriceK. Neighborhood doesn’t explain all of the variation in home prices (there still is error), but it does appear to explain some.

Quantifying the Neighborhood Model

In the previous chapter we developed our first real statistical model, the empty model. As it turned out, the best prediction of a future home sale if we know nothing about the home is just the mean of the outcome variable PriceK. We called this empty model a one-parameter model because our prediction was based on a single estimate: the mean.

Let’s see if we can follow a similar approach to going from our informal Neighborhood model expressed as a word equation, to a true statistical model that we can use to predict the prices for future home sales.

We can turn the neighborhood model into a statistical model in much the same way we did for the empty model. This time, instead of predicting the next home price to be the mean of PriceK we will predict it to be the mean price given its neighborhood. Thus, if the home is in College Creek we will predict its price as the mean of College Creek, and if in Old Town, the mean of Old Town.

This is a two-parameter model, because it will require us to make two estimates, one for each neighborhood. We have added a visualization of the Neighborhood model to the plot below (the firebrick horizontal lines), in addition to a visualization of the empty model (the blue horizontal line). (We’ll teach you the code to make this yourself a little later.)

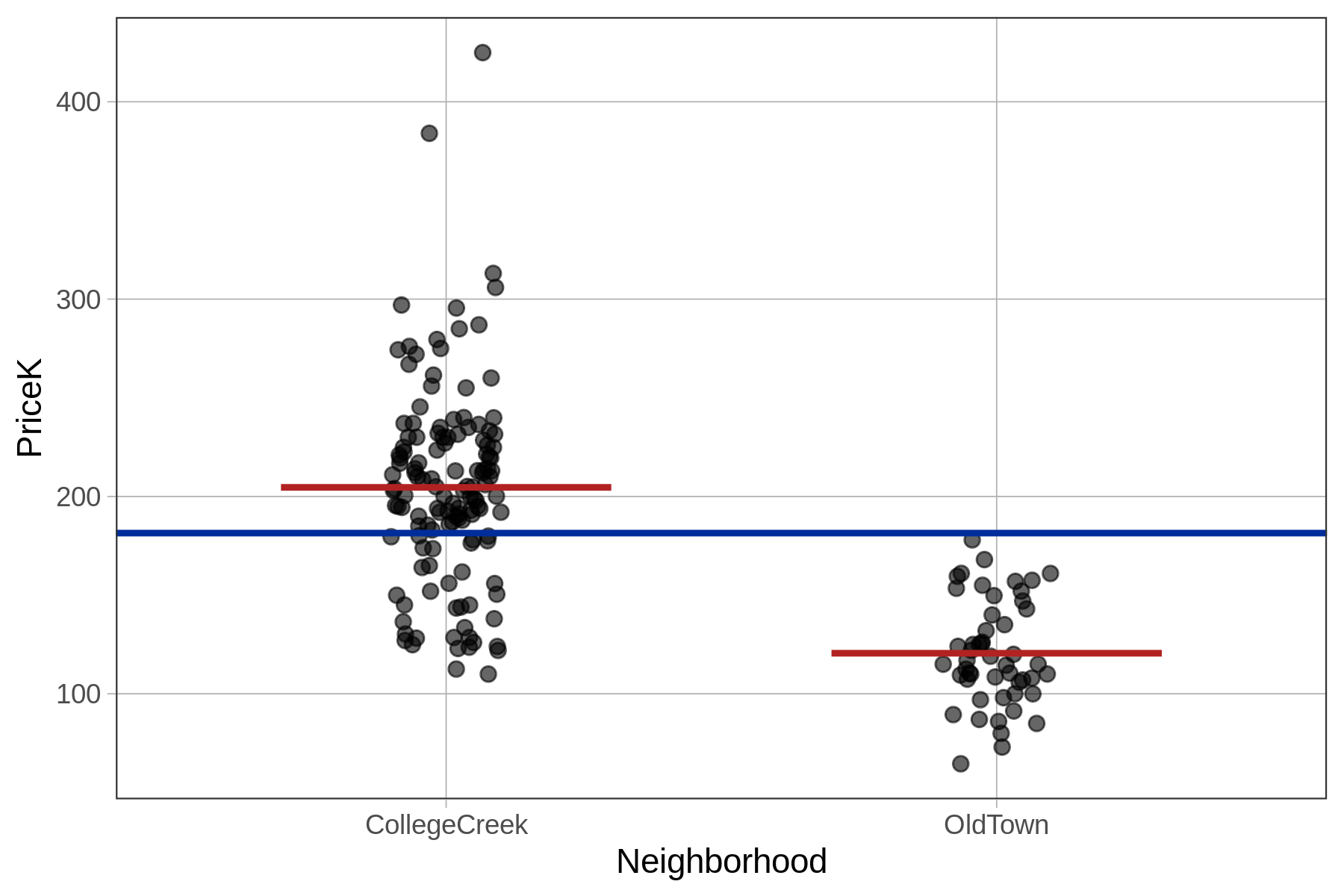
In the following pages we will learn how to use R to fit the Neighborhood model to the Ames data; how to interpret the parameter estimates; how to write the model in GLM notation; how to quantify error around the model; and how to compare the model to the empty model.