Course Outline

list High School / Advanced Statistics and Data Science I (ABC)

Book
  • High School / Advanced Statistics and Data Science I (ABC)
  • High School / Statistics and Data Science I (AB)
  • High School / Statistics and Data Science II (XCD)
  • College / Statistics and Data Science (ABC)
  • College / Advanced Statistics and Data Science (ABCD)
  • College / Accelerated Statistics and Data Science (XCDCOLLEGE)
  • Skew the Script: Jupyter

7.5 Error Leftover From the Group Model

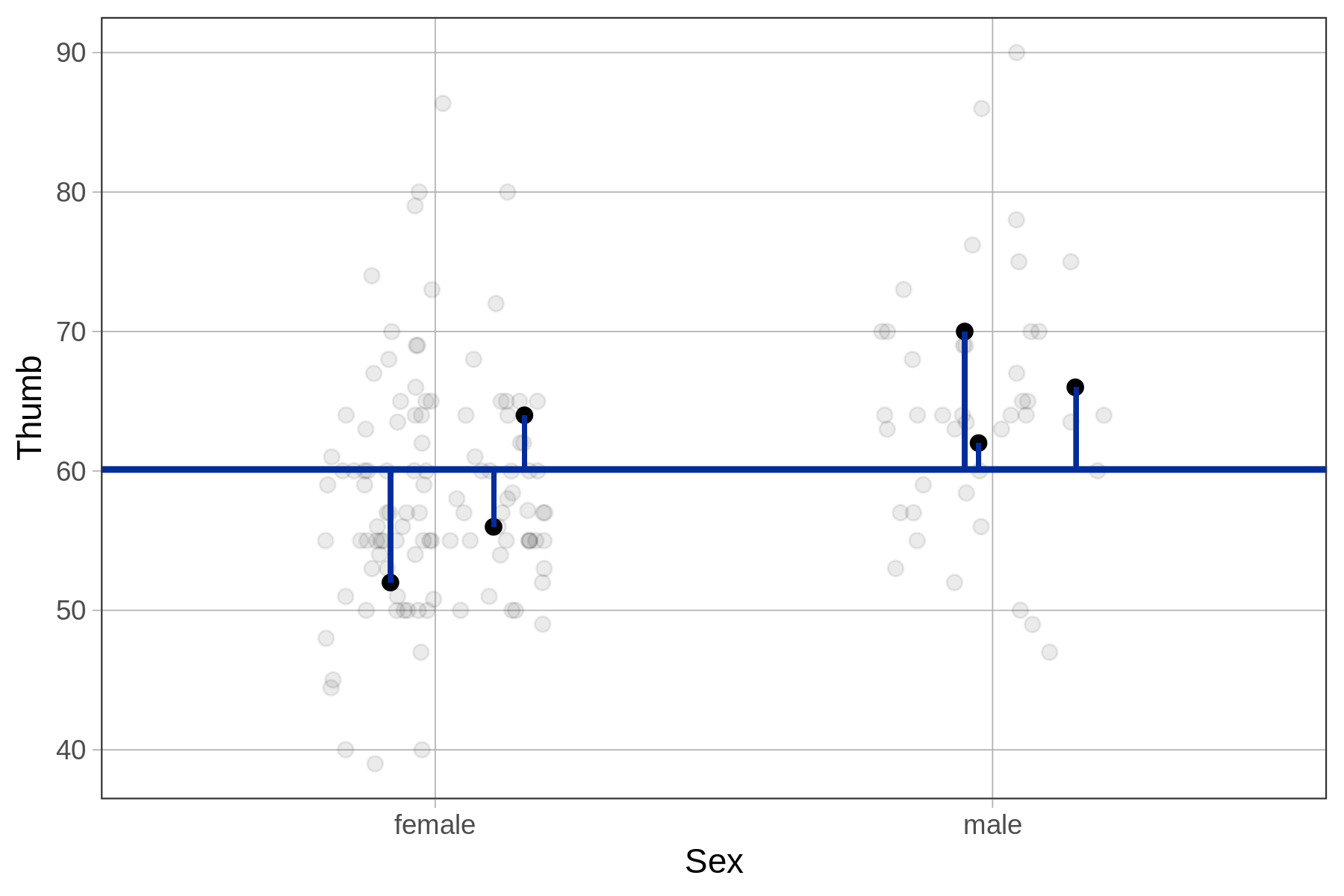
Previously, we calculated residuals from the empty model of Thumb by starting with the actual thumb length for each student, and then subtracting the predicted value based on the model. In the empty model, all students had the same predicted value.

DATA = MODEL PREDICTION + RESIDUAL

RESIDUAL = DATA - MODEL PREDICTION

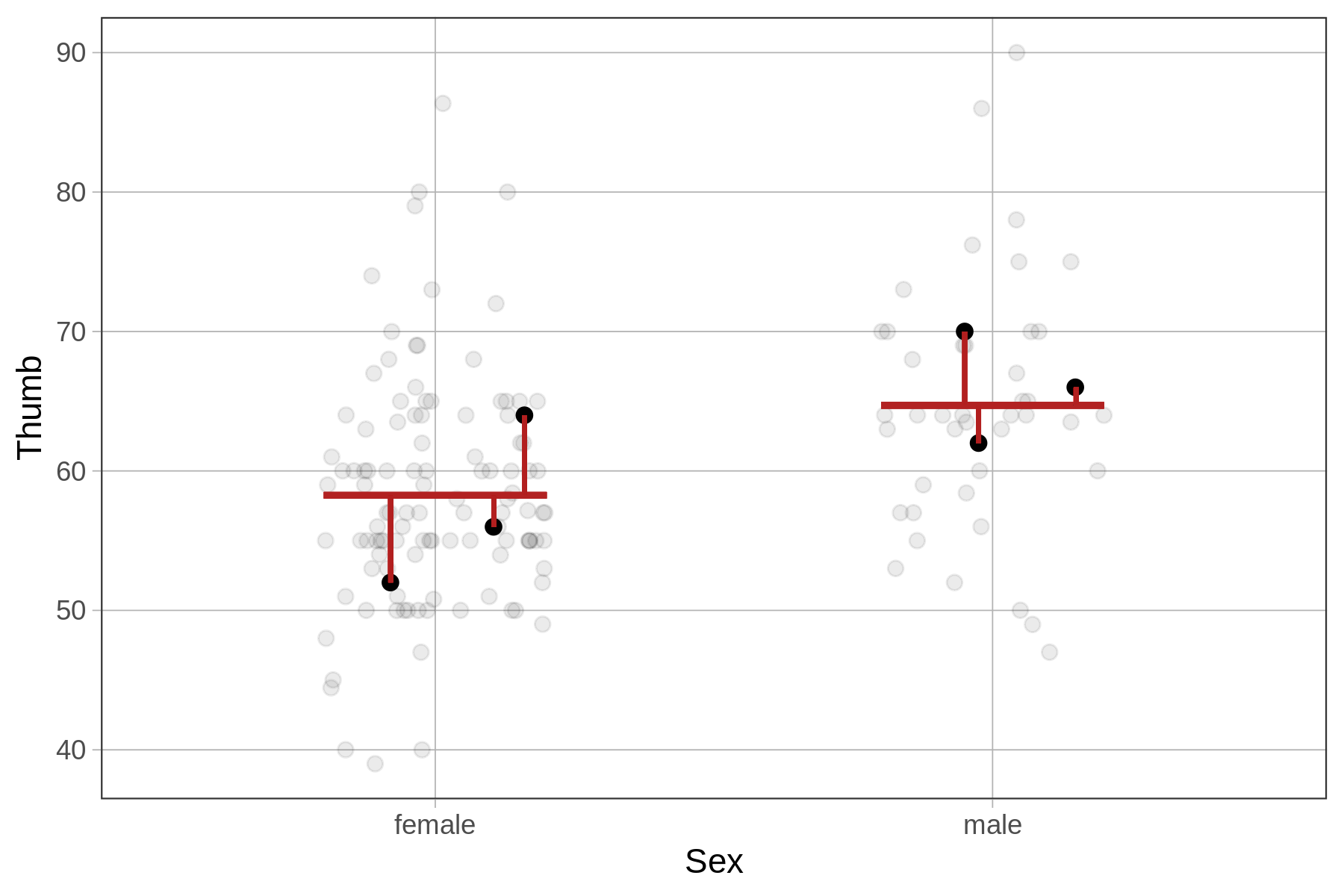
For the Sex model of Thumb we will use the same method, the only difference being that this time there will be two different model predictions, depending on the sex of the student. Still, the predicted thumb length for each student, which depends on their sex, is subtracted from their actual thumb length to get the residuals.

The residuals for 6 example students are represented in the plots below for both the empty model (left) and Sex model (right). Notice that the placement of the 6 data points is the same from one model to the other; the actual thumb lengths of these students don’t change.

Residuals from the Empty Model Residuals from the Sex Model

On the left, a jitter plot of the distribution of Thumb by Sex, overlaid with a horizontal line in blue showing the empty model for Thumb. A few residuals are drawn above and below the empty model as vertical lines from the data points to the model. The plot caption reads: Residuals from the Empty Model.

On the right, a jitter plot of the distribution of Thumb by Sex, overlaid with a red horizontal line in each group showing the group mean. The residuals of the same few data points from the jitter plot on the left are drawn above and below the mean lines as vertical lines from the data points to the mean lines. The plot caption reads: Residuals from the Sex model.

The predictions and residuals of the two models, however, are different. For the empty model, each student’s residual is calculated in relation to the mean Thumb of all students in the data set. For the Sex model, each student’s residual is calculated in relation to the predicted Thumb for their sex.

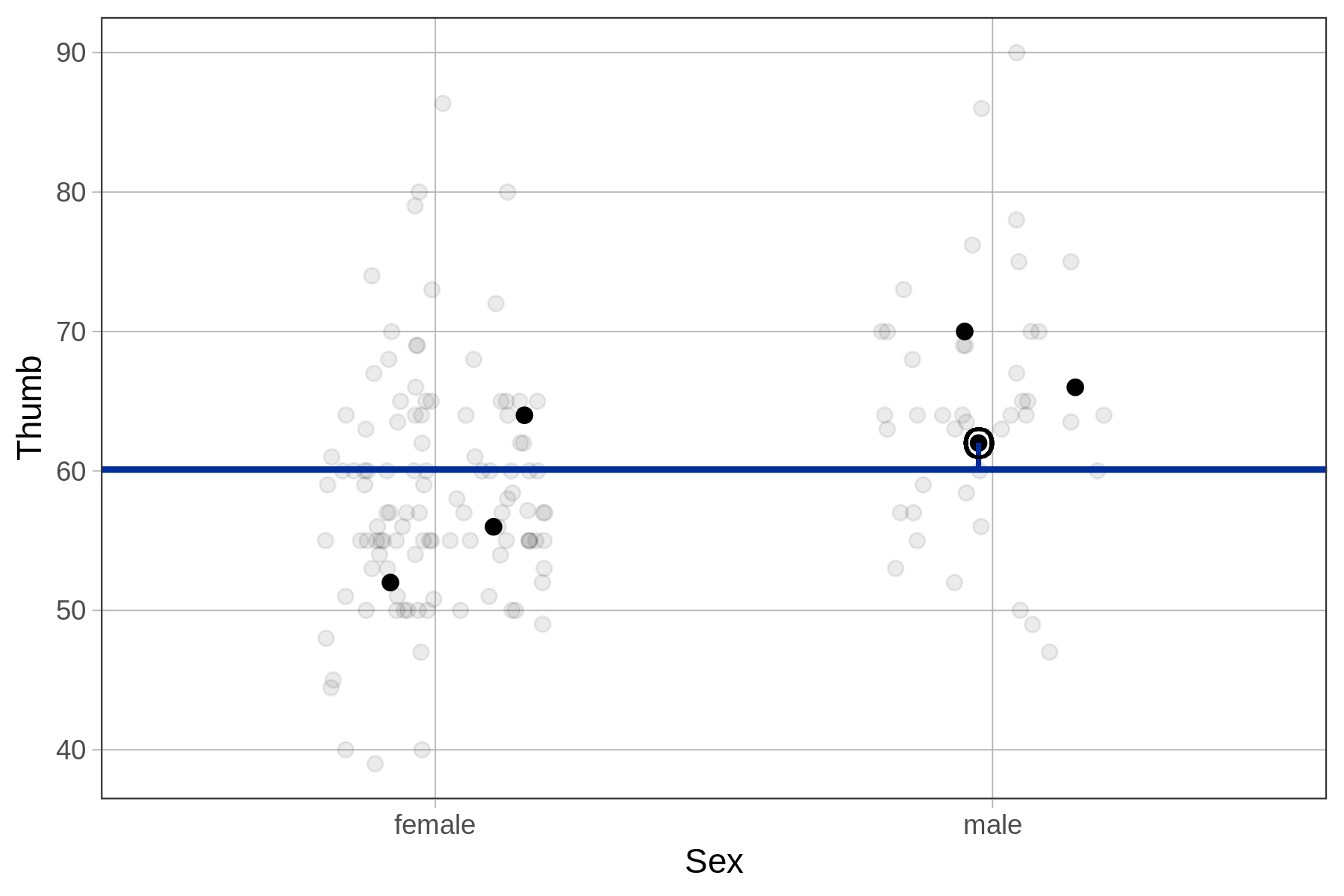
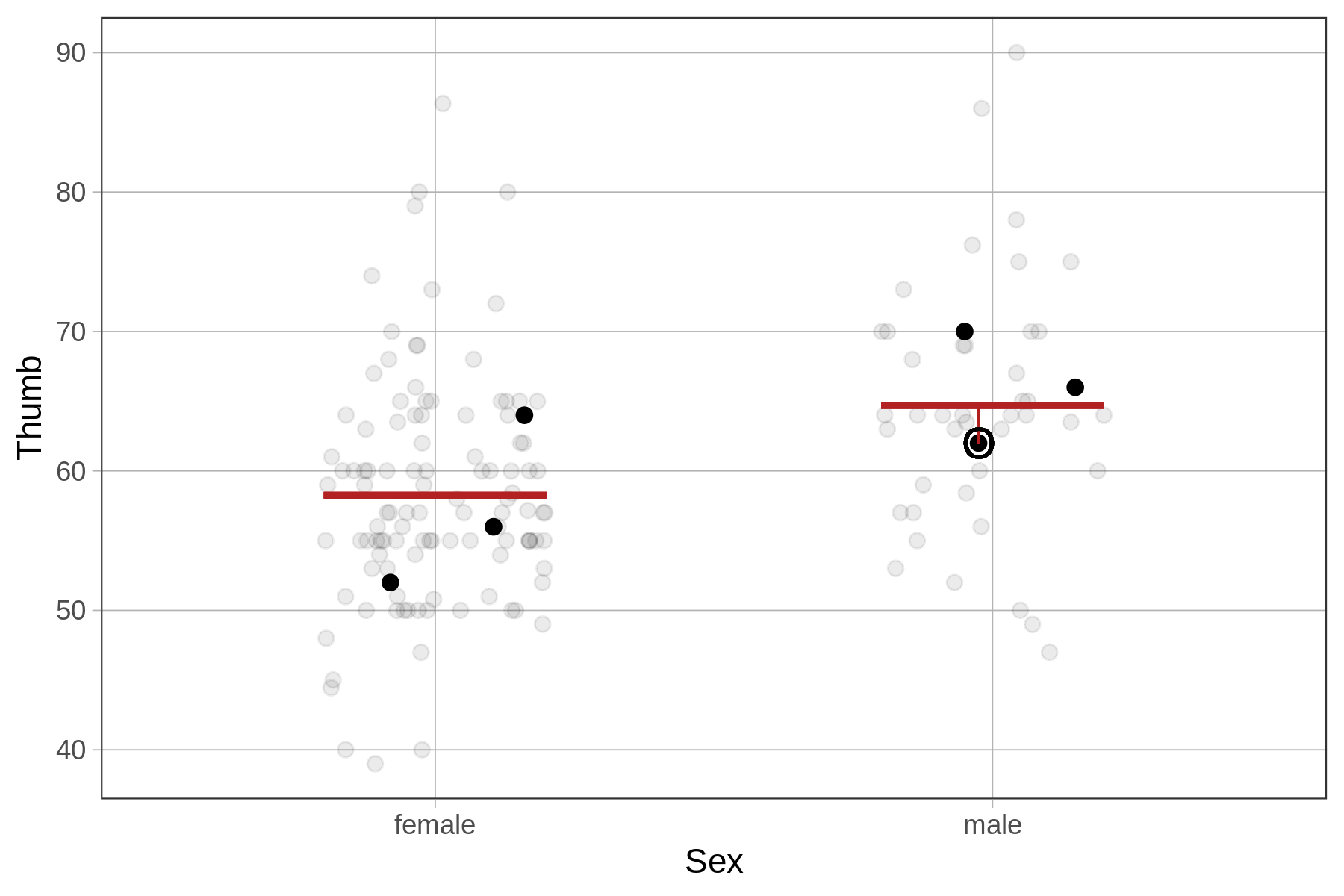
Something to keep in mind as well is that looking at residuals can help you interpret your data. Take, for example, the male student whose thumb length is circled in the plots below. Looking at residuals can help you see something interesting about this student.

In relation to the empty model, this student has a larger than average thumb length. In relation to the sex model, the same student has a slightly below average thumb length given that they are male.

On the left, a jitter plot of the distribution of Thumb by Sex, overlaid with a horizontal line in blue showing the empty model for Thumb. A single residual in the male group is drawn above the empty model as a vertical line from the data point to the model.

On the right, a jitter plot of the distribution of Thumb by Sex, overlaid with a red horizontal line in each group showing the group mean. The residual for the same data point as in the jitter plot on the left appears is now below the line for the male group.


Using R to Calculate Residuals from the Sex Model

Just as we earlier used the predict() function to generate a predicted thumb length to each student in the data frame, we can use the resid() function to calculate the residual for each student. We’ve done that with the code below, and printed out the data table for just the 6 students we have been looking at.

Fingers$Sex_predict <- predict(Sex_model)
Fingers$Sex_resid <- resid(Sex_model)
head(select(Fingers, Sex, Thumb, Sex_predict, Sex_resid))
     Sex Thumb Sex_predict Sex_resid
1 female    64    58.25585  5.744152
2 female    56    58.25585 -2.255848
3 female    52    58.25585 -6.255848
4   male    66    64.70267  1.297333
5   male    70    64.70267  5.297333
6   male    62    64.70267 -2.702667

Responses

Responses
close