Course Outline

list High School / Statistics and Data Science II (XCD)

Book
  • High School / Advanced Statistics and Data Science I (ABC)
  • High School / Statistics and Data Science I (AB)
  • High School / Statistics and Data Science II (XCD)
  • College / Statistics and Data Science (ABC)
  • College / Advanced Statistics and Data Science (ABCD)
  • College / Accelerated Statistics and Data Science (XCDCOLLEGE)
  • Skew the Script: Jupyter

3.9 Error from the HomeSizeK Model

Regardless of model, error from the model (or residuals) are always calculated the same way for each data point:

\[residual=observed\ value - predicted\ value\]

For regression models, the predicted value of \(Y_i\) will be right on the regression line. Error, therefore, is calculated based on the vertical gap between a data point’s value on the Y axis (the outcome variable) and its predicted value based on the regression line.

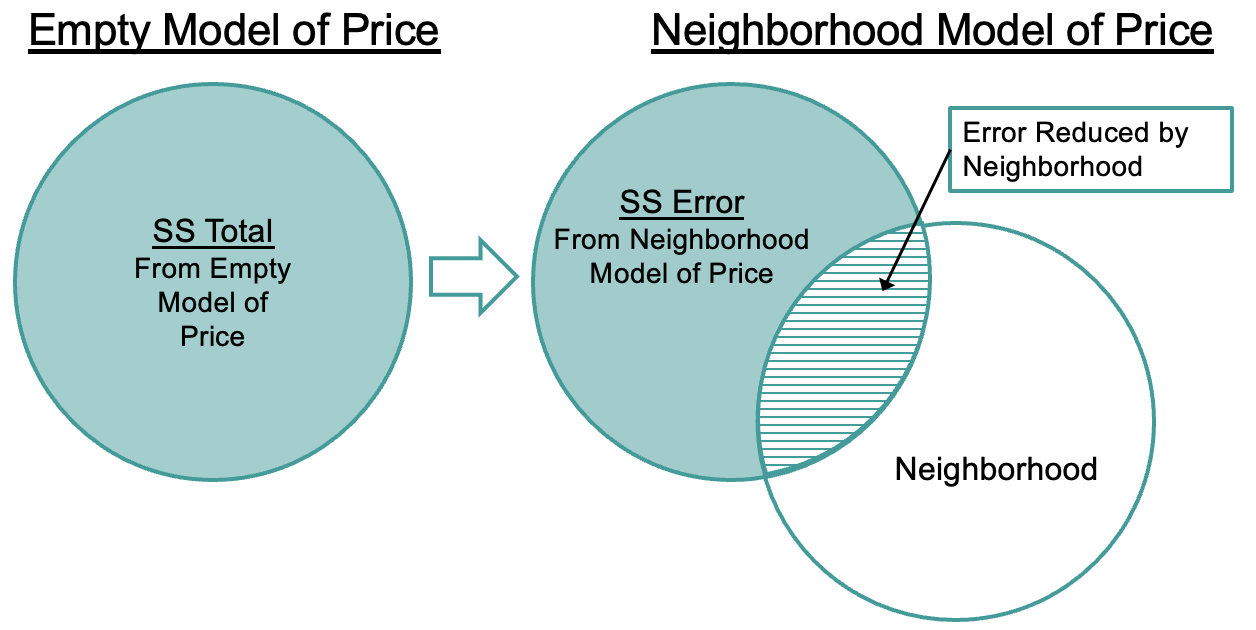
Below we have depicted just 6 data points (in black) and their residuals (firebrick vertical lines) from the HomeSizeK model.

A scatterplot of the distribution of PriceK by HomeSizeK in the Ames data frame, overlaid with the regression line in red. A few residuals are drawn above and below the regression line as vertical lines from the data points to the model.

Note that a negative residual (shown below the regression line) means that the data (e.g., PriceK) was lower than the predicted price given the home’s size.

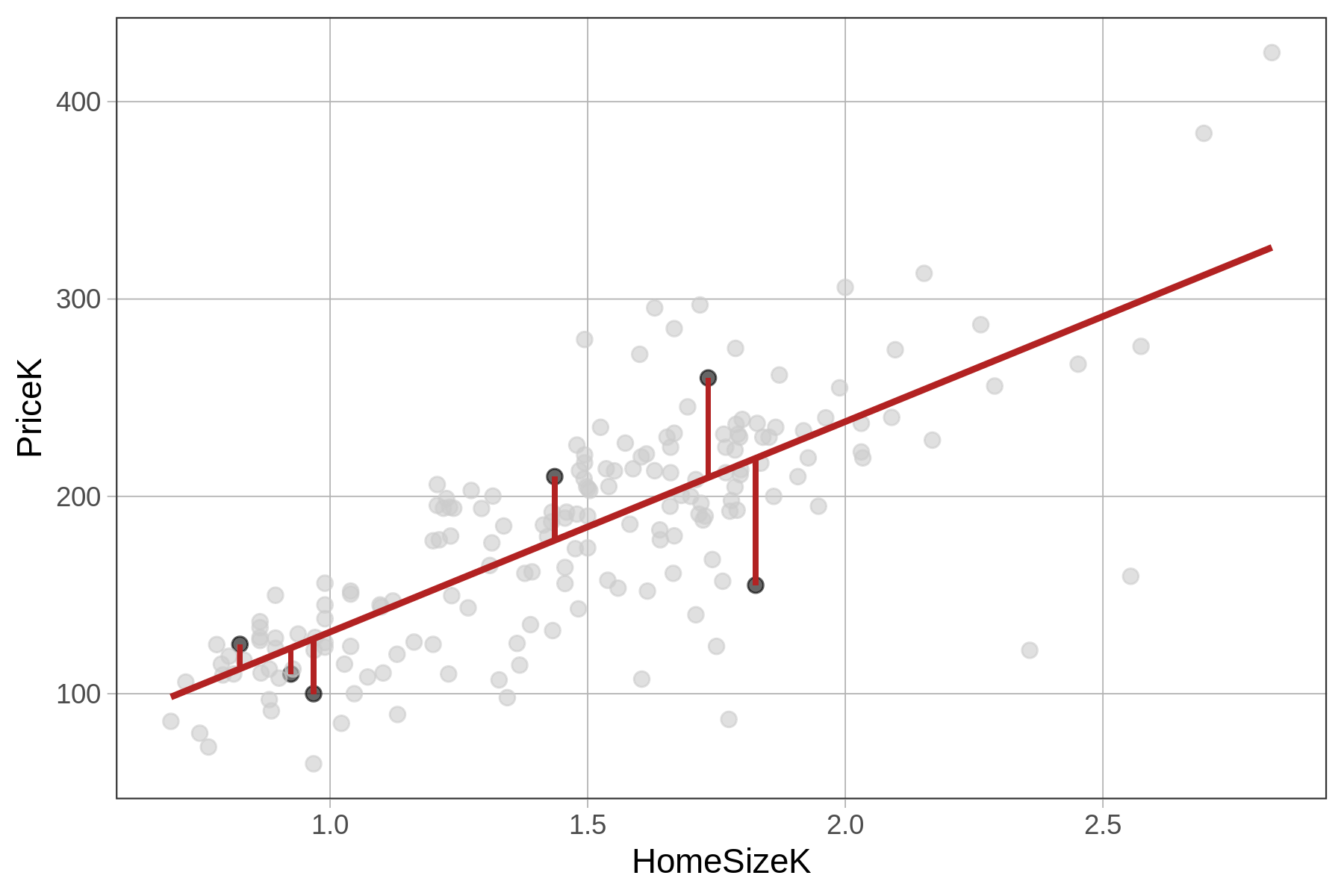
The residuals from the HomeSizeK model represent the variation in PriceK that is leftover after we take out the part that can be explained by HomeSizeK. As an example, take a particular house (highlighted in the plot below) that sold for $260K. The residual of 50 means that the house sold for $50K more than would have been predicted based on its size.

A scatterplot of the distribution of PriceK by HomeSizeK in the Ames data frame, overlaid with the regression line in red. A single residual is drawn above the regression line as a vertical line from the data point to the model. The data point is labeled as: PriceK equals 260. The vertical line is labeled as: residual equals 50. The point along the regression line is labeled as: predicted PriceK equals 210.

Another way we could say this is: Controlling for home size, this house sold for $50K more than expected. A positive residual indicates that a house is expensive for its size. A negative residual indicates that a house is cheap for its size (maybe prompting us to ask – “Hey! What’s wrong with it?”).

SS Error for the HomeSizeK Model

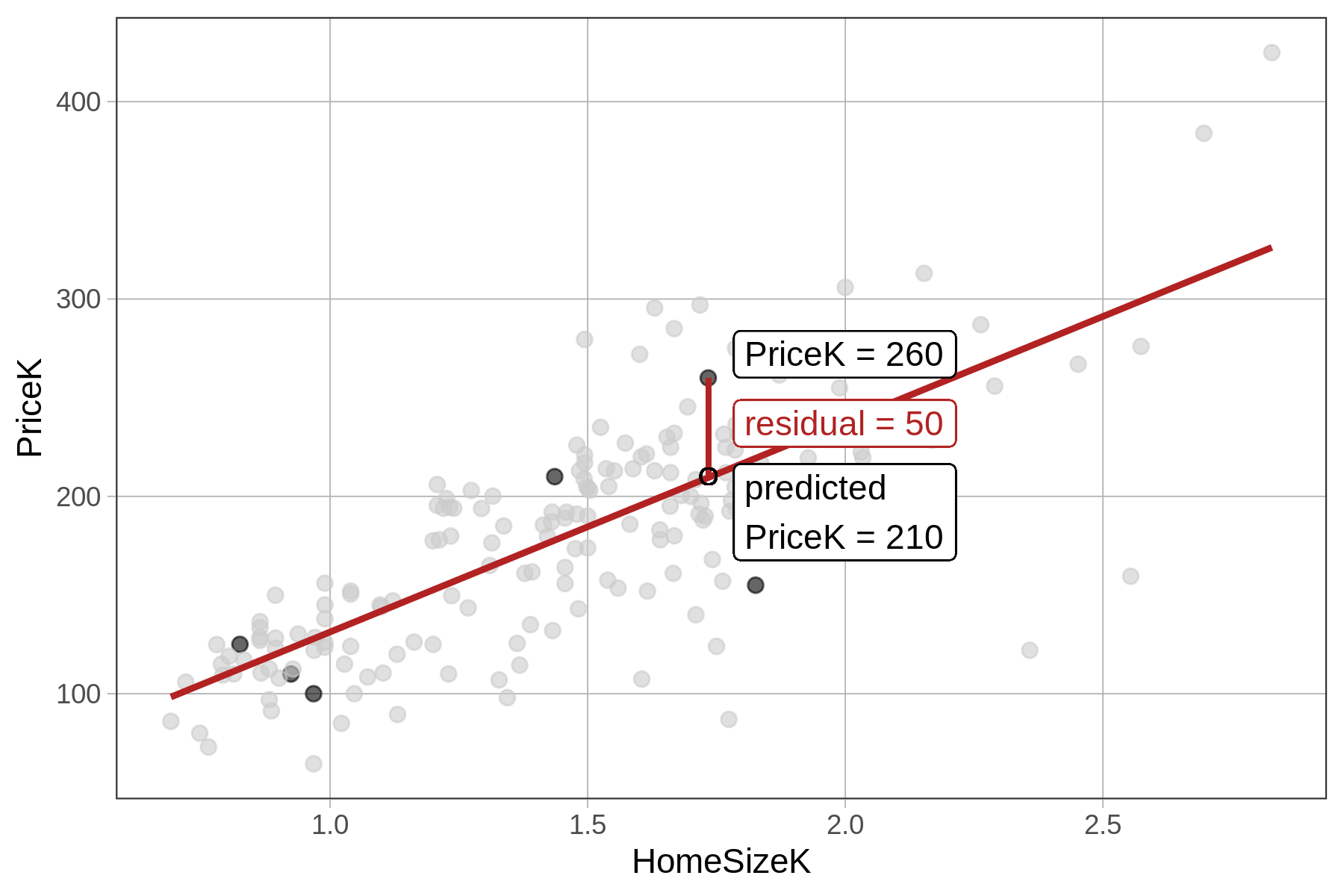
Just like for the Neighborhood model, the metric we use for quantifying total error from the HomeSizeK model is the sum of squared residuals from the model, or SS Error. The sum of squares is calculated from the residuals in the same way as it is for the Neighborhood model, by squaring and then summing the residuals (see figure below).

A scatterplot of the distribution of PriceK by HomeSizeK in the Ames data frame, overlaid with the regression line in red. A few squared residuals are drawn above and below the regression model as vertical lines from the data points to the model that have been scaled into squares.

Using R to Compare SS for the HomeSizeK Model and the Empty Model

Just like we did with the Neighborhood model, we can use the resid() function to get the residuals from the HomeSizeK model. We can square them and sum them to get the SS Error from the model like this:

HomeSizeK_model <- lm(PriceK ~ HomeSizeK, data = Ames)
sum(resid(HomeSizeK_model)^2)

The code below will calculate SST from the empty model and SSE from the home size model. Run it to check your predictions about SSE.

require(coursekata) # this calculates SST empty_model <- lm(PriceK ~ NULL, data=Ames) print("SST") sum(resid(empty_model)^2) # this calculates SSE HomeSizeK_model <- lm(PriceK ~ HomeSizeK, data = Ames) print("SSE") sum(resid(HomeSizeK_model)^2) # no test ex() %>% check_error()
CK Code: X3_Code_ErrorH_01
[1] "SST"
633717.215434616
 
[1] "SSE"
258952.710665327

Notice that the SST is the same as it was for the Neighborhood model: 633,717. This is because the empty model hasn’t changed, assuming that the same data points go into each analysis; SST is still based on residuals from the grand mean of PriceK. The SSE (258,952) is smaller than SST because the residuals are smaller (as represented in the figures above by shorter lines). Squaring and summing smaller residuals results in a smaller SSE. The total error has been reduced quite a bit by this regression model.

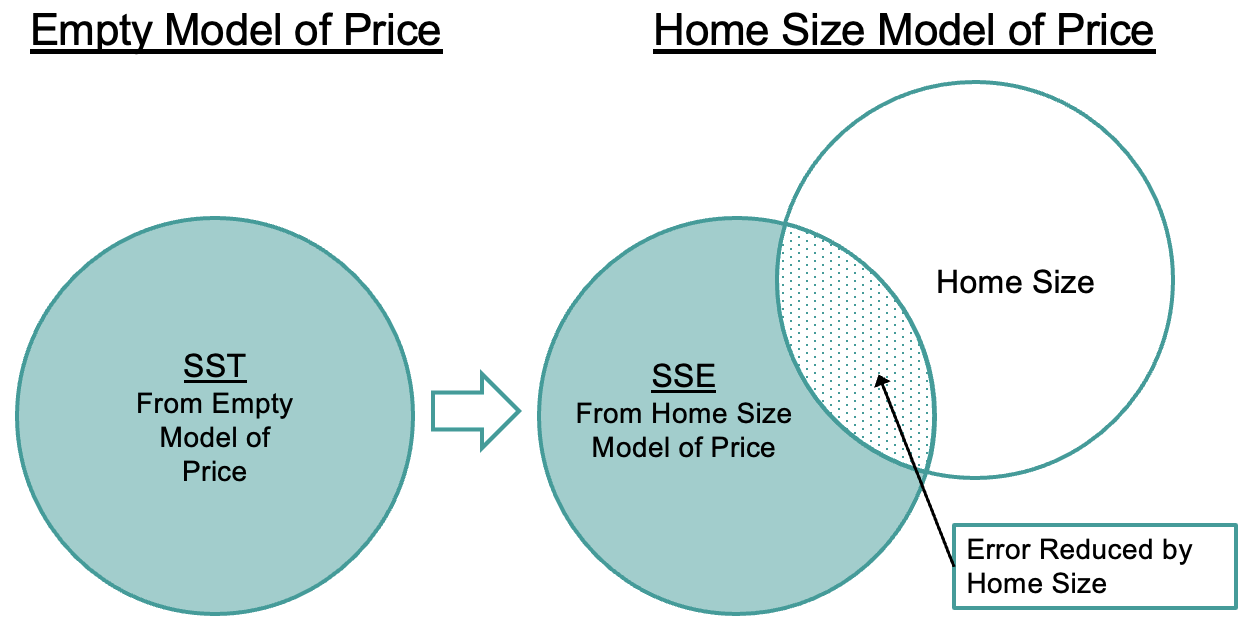
Diagram showing the partitioning of Sum of Squares. On the left, a single circle represents SS Total from the Empty Model of Price. An arrow from that circle points to a Venn diagram of two partially overlapping circles to the right. One circle is labeled as SS Error from the Home Size Model of Price, and the other circle is labeled as Home Size. The intersection where the two circles overlap is labeled as Error Reduced by Home Size.

We’ve been talking about the SS Total and SS Error in relation to the HomeSizeK model. Let’s shift back to considering the Neighborhood model. Notice that in both models, we are partitioning SST into two parts: the part of SST that has been reduced by the model (which we will discuss more on the next page); and SSE, which is the amount of error still leftover after applying the model.

Diagram showing the partitioning of Sum of Squares Total similar to the figure above. Instead of the HomeSizeK model of Price, the partition of Sum of Squares is by the Neighborhood model of Price.

Responses

Responses
close