CourseKata - 11.2 Using Bootstrapping to Calculate the 95% Confidence Interval

High School / Advanced Statistics and Data Science I (ABC)

Book

11.2 Using Bootstrapping to Calculate the 95% Confidence Interval

Sliding a visualization up and down is a good way to understand the concept behind confidence intervals, but it’s not a very good way to calculate the actual upper and lower bounds! In this section we will learn one method (among many) to calculate a confidence interval.

In sliding the sampling distribution around, we’re making a few assumptions. We assume, first, that the shape and spread of the sampling distribution does not change as we slide it up and down the measurement scale. The sampling distribution is roughly normal for $b_1$, which means it is unimodal and symmetrical, with a tail on either end.

We are also going to assume that the center of the confidence interval is at the observed sample $b_1$ (e.g., $6.05 in the tipping study). We can convince you of this, we hope, using the picture below. We have re-colored the sampling distribution centered at $6.05 in red. We also drew in two dotted black lines indicating the cutoffs that separate the likely and unlikely area of that sampling distribution. Behind it are the distributions we used to find the upper and lower bounds.

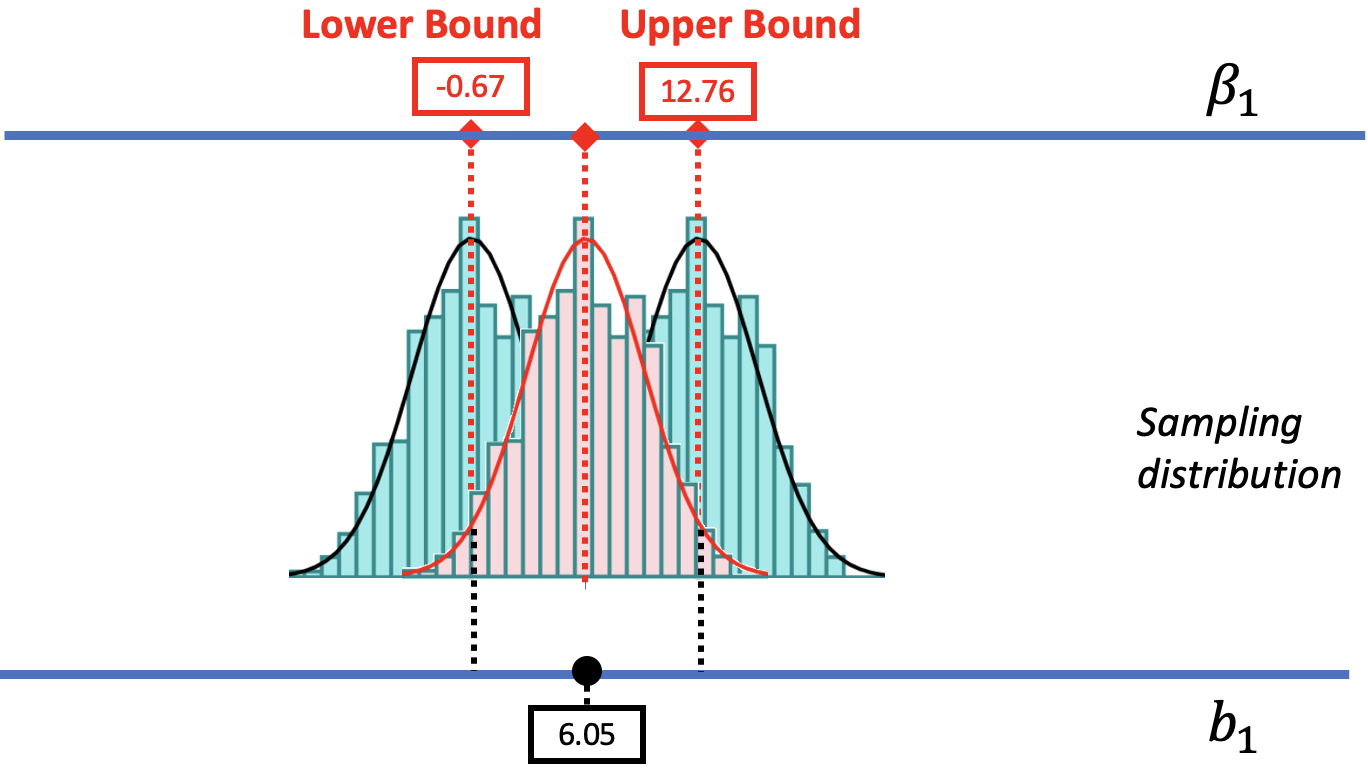
The .025 cutoff in the lower tail of the sampling distribution centered at the sample $b_1$ lines up perfectly with the lower bound of the confidence interval. Likewise, the .025 cutoff in the upper tail lines up with the upper bound of the confidence interval. If only we had a sampling distribution centered at $b_1$, we would be able to figure out the lower and upper bounds.

Bootstrapping with `resample()`

For calculating the confidence interval, it would be helpful to have a sampling distribution centered at the sample $b_1$. Unfortunately, the shuffle() function, which mimics a DGP where $\beta_1=0$, produces a sampling distribution that is centered at 0. But we need to mimic a DGP where the $\beta_1$ is equal to our sample $b_1$ (6.05).

We can do this using the resample() function. The resample() function assumes that the entire population of interest is made up of observations that look just like the ones in our sample. In the case of the tipping experiment, we would assume a population made up of many copies of the tables in the TipExperiment sample.

By repeatedly sampling from this imaginary population, we can create a sampling distribution of $b_1$s that will be centered at the observed sample $b_1$. This approach to creating a sampling distribution is sometimes called bootstrapping.

We previously used the resample() function with a vector (just a list of numbers) to simulate dice rolls. In bootstrapping, we will resample cases from a data frame instead of numbers from a vector.

To illustrate how this works, let’s focus on a subgroup of 6 tables from the TipExperiment data frame. We have put these six tables in a new data frame called SixTables. The output below shows the contents of this data frame.

  TableID Tip   Condition
        4  34     Control
       18  21     Control
       43  21 Smiley Face
        6  31     Control
       25  47 Smiley Face
       35  27 Smiley Face

Notice that in our small sample of 6 tables, there are 3 tables in the Smiley Face condition and 3 in the Control condition.

Now let’s see what happens when we resample() from this sample of 6 tables.

resample(SixTables)

In the table below, we’ve put the original 6 tables on the left, and the results of the resample() function on the right.

Original 6 Tables Resampled 6 Tables

Original 6 Tables	Resampled 6 Tables
`TableID Tip Condition 4 34 Control 18 21 Control 43 21 Smiley Face 6 31 Control 25 47 Smiley Face 35 27 Smiley Face`	`TableID Tip Condition 43 21 Smiley Face 6 31 Control 18 21 Control 6 31 Control 18 21 Control 35 27 Smiley Face`

  TableID Tip   Condition
        4  34     Control
       18  21     Control
       43  21 Smiley Face
        6  31     Control
       25  47 Smiley Face
       35  27 Smiley Face

  TableID Tip   Condition
       43  21 Smiley Face
        6  31     Control
       18  21     Control
        6  31     Control
       18  21     Control
       35  27 Smiley Face

The resample() function takes a new random sample of six tables from the data set. It samples with replacement, meaning that when R randomly samples a table, it then puts the table back so it could potentially be sampled again. This explains why a table in the original data might appear more than once, or perhaps not at all, in the resampled data.

Okay, enough already with just six tables!

Let’s now use resample() to bootstrap a new sample of 44 tables from the tables in the tipping study. Later, we will repeat this process many times to bootstrap a sampling distribution of $b_1$s. Let’s start by thinking about what would happen if you ran the following line of code on the complete TipExperiment data frame:

resample(TipExperiment)

Both the resampled and original data frames will have 44 tables. However, because some tables might be selected more than once in the resampled data frame, and others not at all, the number of tables in each condition won’t exactly match the numbers in the original data frame. (We aren’t going to worry about this for now.)

We can also see that the average Tip for each condition will be different in the resampled data frame. This makes sense because the exact tables included are not the same in the two data frames.

Use the code window below to produce the $b_1$ estimate for the Condition model of Tip in both the original and resampled data frames. Run the code a few times, and see what you notice.

require(coursekata)

# run this a few times
b1(Tip ~ Condition, data = TipExperiment)
b1(Tip ~ Condition, data = resample(TipExperiment))

# no solution; commenting for submit button

ex() %>% check_error()

CK Code: ch11-02-01-code

Each time you run the code you will get two $b_1$s printed out. The first is based on the original data frame, and will always be $6.05; we know this by now! But the second $b_1$ will vary each time you run the code. This is because each time you run the code, R is calculating the mean difference between smiley face and control group in a new resampled version of the data frame.

Using Resample() to Bootstrap a Sampling Distribution

Now that we have reviewed how the resample() function works, let’s use it to create a sampling distribution of 1000 $b_1$s.

Modify the code in the window below to create a sampling distribution of 1000 $b_1$s, each based on resampled data, and save it into a new data frame called sdob1_boot. Add some code to produce a histogram of the sampling distribution.

require(coursekata)

# modify this to make 1000 bootstrapped b1s
sdob1_boot <- do( ) * b1(Tip ~ Condition, data = resample(TipExperiment))

# visualize sdob1_boot with a histogram

# modify this to make 1000 bootstrapped b1s
sdob1_boot <- do(1000) * b1(Tip ~ Condition, data = resample(TipExperiment))

# visualize sdob1_boot with a histogram
gf_histogram(~b1, data = sdob1_boot)

ex() %>% {
       check_function(., "do") %>%
           check_arg("object") %>%
           check_equal()
       check_or(.,
           check_function(., "gf_histogram") %>% {
               check_arg(., "object") %>% check_equal()
               check_arg(., "data") %>% check_equal()
           },
           override_solution_code(., '{
               sdob1_boot <- do(1000) * b1(Tip ~ Condition, data = resample(TipExperiment))
               gf_histogram(sdob1_boot, ~b1)
           }') %>%
               check_function(., "gf_histogram") %>% {
                   check_arg(., "object") %>% check_equal()
                   check_arg(., "gformula") %>% check_equal()
               },
           override_solution_code(., '{
               sdob1_boot <- do(1000) * b1(Tip ~ Condition, data = resample(TipExperiment))
               gf_histogram(~sdob1_boot$b1)
           }') %>%
               check_function(., "gf_histogram") %>% {
                   check_arg(., "object") %>% check_equal()
               }
       )
   }

CK Code: ch11-02-02-code

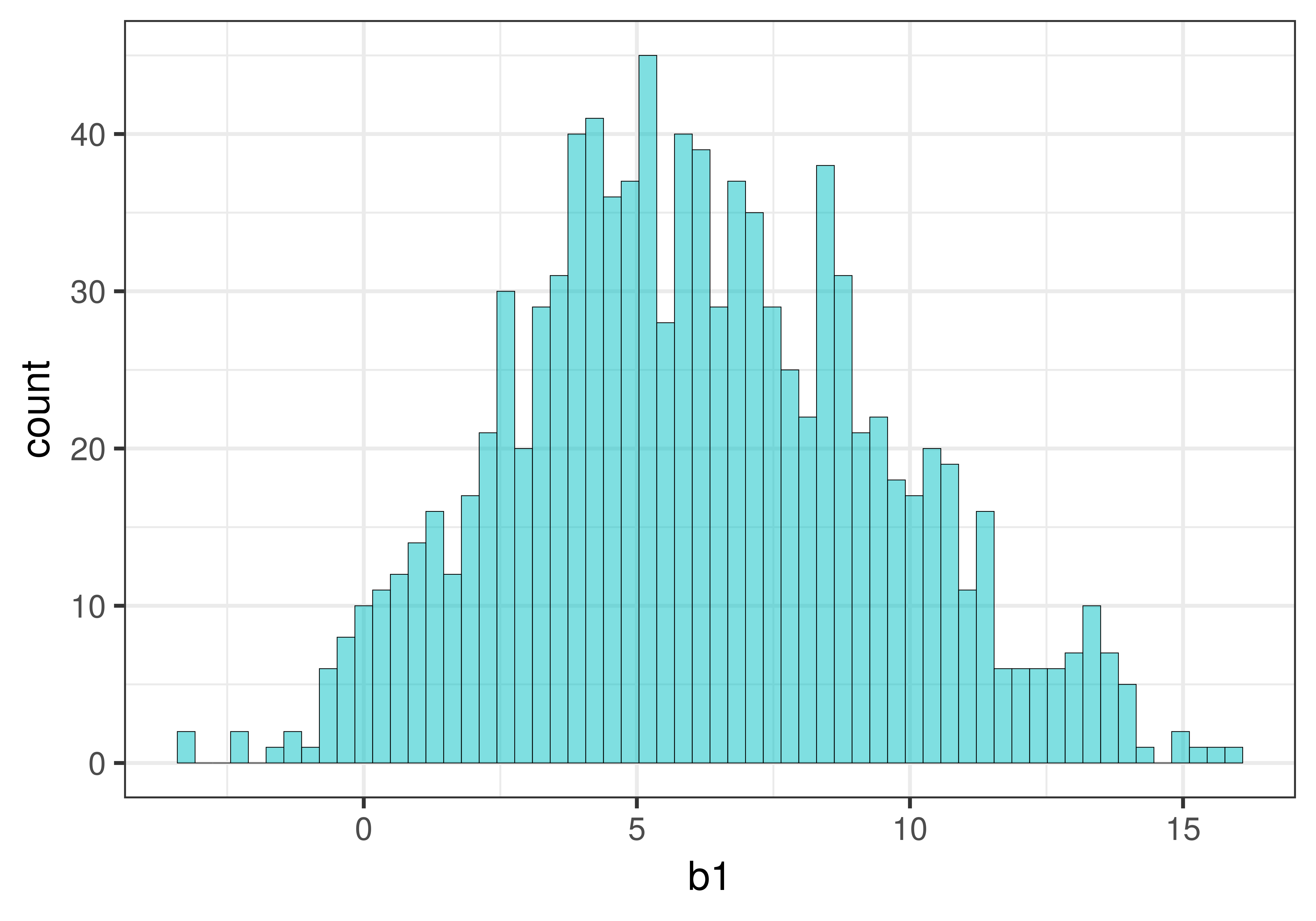
A histogram of the sampling distribution of b1. It is normally distributed, and centered around 5 or 6. The distribution ranges along the x-axis from about negative 3 to about 16.

Use favstats() in the code window below to see what the average of the $b_1$s is in sdob1_boot.

require(coursekata)

# we have created the sampling distribution for you
sdob1_boot <- do(1000) * b1(Tip ~ Condition, data = resample(TipExperiment))

# run favstats to check out the mean of the sampling distribution

# we have created the sampling distribution for you
sdob1_boot <- do(1000) * b1(Tip ~ Condition, data = resample(TipExperiment))

# run favstats to check out the mean of the sampling distribution
favstats(~b1, data = sdob1_boot)

ex() %>%
       check_function("favstats") %>%
       check_result() %>%
       check_equal()

CK Code: ch11-02-03-code

       min       Q1   median       Q3      max     mean       sd    n missing
 -3.219048 3.772727 5.921166 8.480083 15.96154 6.110566 3.381418 1000       0

The mean is fairly close to $6.05, the estimate of $\beta_1$ from the tipping study. Because the resampled sampling distribution is roughly centered at the sample $b_1$, it provides us what we were looking for in order to calculate the 95% confidence interval for $\beta_1$: a sampling distribution centered at the sample $b_1$.

Using the Bootstrapped Sampling Distribution to Find the Confidence Interval

We have now succeeded in creating a bootstrapped sampling distribution of 1000 $b_1$s centered at the sample $b_1$ (roughly $6.05) using the resample() function. To find the lower and upper bounds of the confidence interval, we will use our sampling distribution of $b_1$s as a probability distribution, interpreting proportions of $b_1$s falling in a certain range as a probability that future $b_1$s would fall into the same range.

We want to find the cutoffs that separate the middle .95 of the resampled sampling distribution from the lower and upper .025 tails because these cutoffs will correspond perfectly with the lower and upper bound of the confidence interval.

To do this, we start by putting the 1000 $b_1$s in order. Then we can find the cutoffs that separate the top 25 and the bottom 25 $b_1$s from the middle 950 $b_1$s.

We can visualize this task by shading in the middle .95 differently from the tails (.025 in each tail) as shown in the histogram below. (The histogram will show all the values of resampled $b_1$ in order from smallest to largest on the x-axis.)

gf_histogram(~b1, data = sdob1_boot, fill = ~middle(b1, .95), bins = 80)

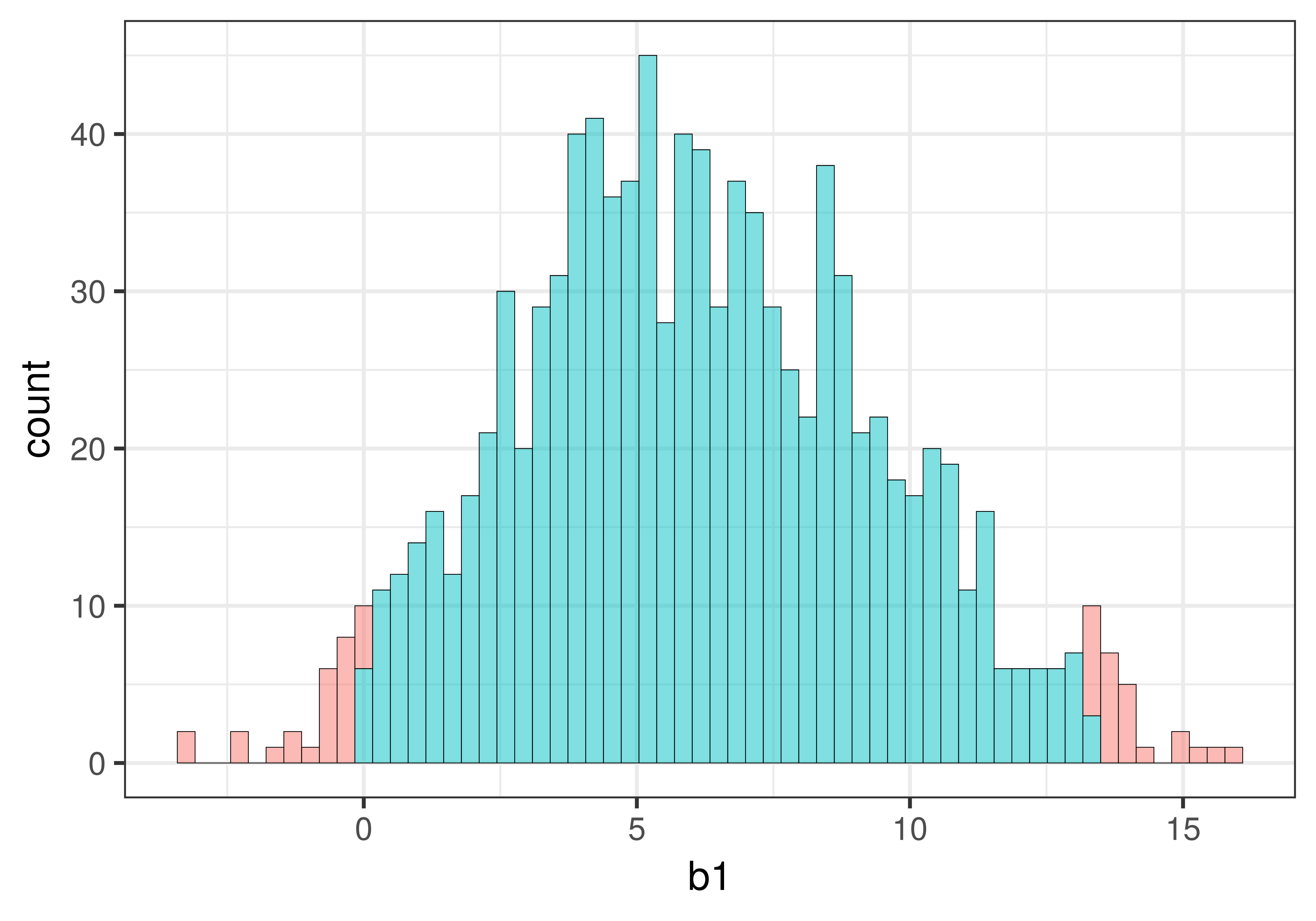
A histogram of the sampling distribution of b1. It is normally distributed, and centered around 5 or 6. The distribution ranges along the x-axis from about negative 3 to about 16. The upper and lower tails of the distribution have been shaded in red. The red area in the lower tail ranges from about negative 3 to zero, and the red area in the upper tail ranges from about 13 to 16.

As illustrated below, the cutoff for the lowest .025 of $b_1$s is at the 26th $b_1$. The cutoff for the highest .025 of $b_1$s is at the 975th $b_1$. These two cutoffs correspond to the lower and upper bound of the confidence interval.

Here’s some code that will arrange the $b_1$s in order (from lowest to highest) and save the re-arranged data back into sdob 1_boot.

sdob1_boot <- arrange(sdob1_boot, b1)

To identify the 26th b1 in the arranged data frame (26th from the lowest), we can use these brackets (e.g., [26]).

sdob1_boot$b1[26]

Use the code block below to print out both the 26th and 975th b1s.

require(coursekata)

sdob1_boot <- do(1000) * b1(Tip ~ Condition, data = resample(TipExperiment))
sdob1_boot <- arrange(sdob1_boot, b1)

# we’ve written code to print the 26th b1
sdob1_boot$b1[26]

# write code to print the 975th b1

# we’ve written code to print the 26th b1
sdob1_boot$b1[26]

# write code to print the 975th b1
sdob1_boot$b1[975]

ex() %>% {
        check_output_expr(., "sdob1_boot$b1[26]")
        check_output_expr(., "sdob1_boot$b1[975]")
}

CK Code: ch11-02-04-code

[1] -0.02484472
[1] 13.3

Based on our bootstrapped sampling distribution of $b_1$, the 95% confidence interval runs from around 0 to 13 (give or take). Your numbers will be slightly different from ours, of course, because they are generated randomly. Based on this analysis, we can be 95% confident that the true value of $\beta_1$ in the DGP lies in this range.

11.1 From Hypothesis Testing to Confidence Intervals 11.3 Shuffle, Resample, and Standard Error

Course Outline

High School / Advanced Statistics and Data Science I (ABC)

11.2 Using Bootstrapping to Calculate the 95% Confidence Interval

Bootstrapping with `resample()`

Using Resample() to Bootstrap a Sampling Distribution

Using the Bootstrapped Sampling Distribution to Find the Confidence Interval

Responses

list High School / Advanced Statistics and Data Science I (ABC)

11.2 Using Bootstrapping to Calculate the 95% Confidence Interval

Bootstrapping with resample()

Using Resample() to Bootstrap a Sampling Distribution

Using the Bootstrapped Sampling Distribution to Find the Confidence Interval

High School / Advanced Statistics and Data Science I (ABC)

Bootstrapping with `resample()`