10.6 Type I and Type II Error
We have said before that statistical models are always wrong. When we compare two models (e.g., the Condition model with the empty model) we try to choose the one that will be less wrong given the data we have. We end up making a decision about what we think the true DGP is. But our decision might be wrong. We won’t know whether it is right or wrong because we never know what the true DGP that produced our data actually is.
Not only might we be wrong, but you may be unsettled to learn that there are at least two different ways you can be wrong when comparing a complex model to the empty model. Statisticians refer to these different ways of being wrong as Type I Error and Type II Error. As we will see, it is very hard to avoid making one or the other of these types of errors.
Type I Error (When Rejecting the Empty Model)
When we have decided to reject the empty model, we may be right or we may be wrong. We may have made the right choice if the empty model really is not true in the DGP. But if the empty model is actually true in the DGP, rejecting the empty model would be a Type I error.
Because we don’t know what the true DGP is, we can never tell whether rejecting the empty model led us to adopt the right model of the DGP or led us to make a Type I error. Whenever we reject the empty model, we need to acknowledge the possibility that we are making a Type I error.
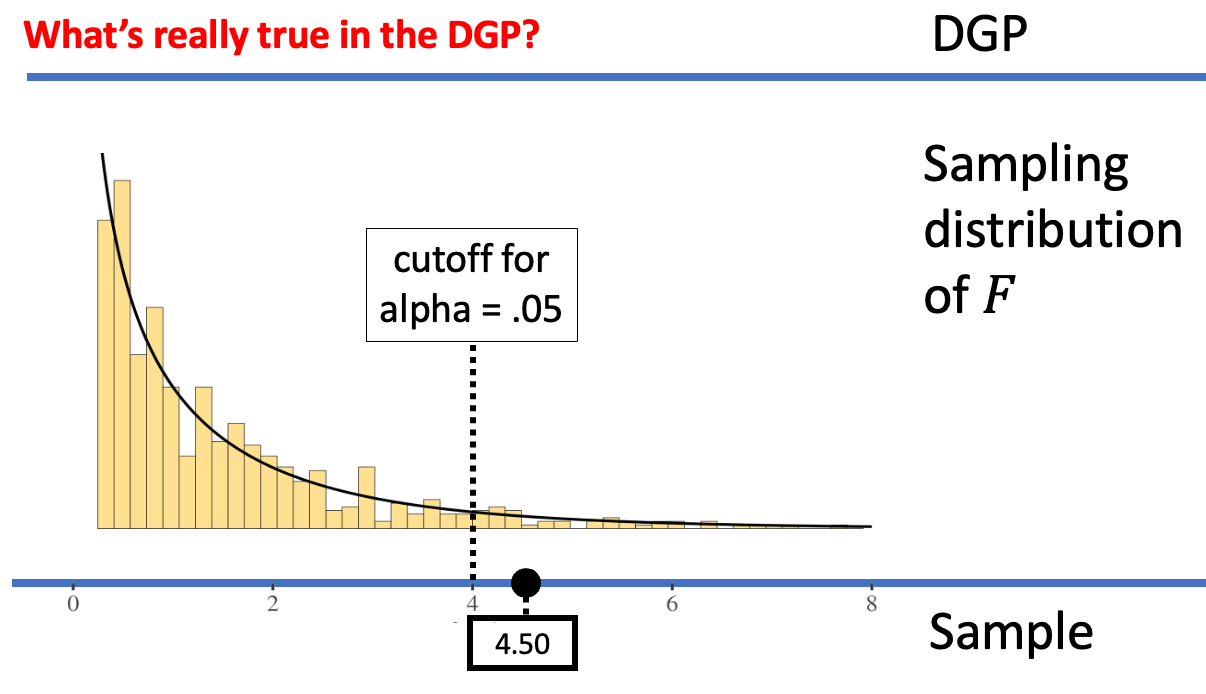
Because the sample F of 4.5 was past the cutoff established by our alpha, we would reject the empty model. But if the empty model were actually true in the DGP, we would have made a Type I error.
Type II Error (When Not Rejecting the Empty Model)
We only make Type I errors when we reject the empty model. Are we in the clear as long as we do not reject the empty model? Unfortunately, not rejecting the empty model leaves open the possibility of another type of error, Type II error, which can only occur when we decide to not reject the empty model.
Although we will never know the true DGP, whenever we do not reject the empty model, we need to acknowledge the possibility of Type II error.
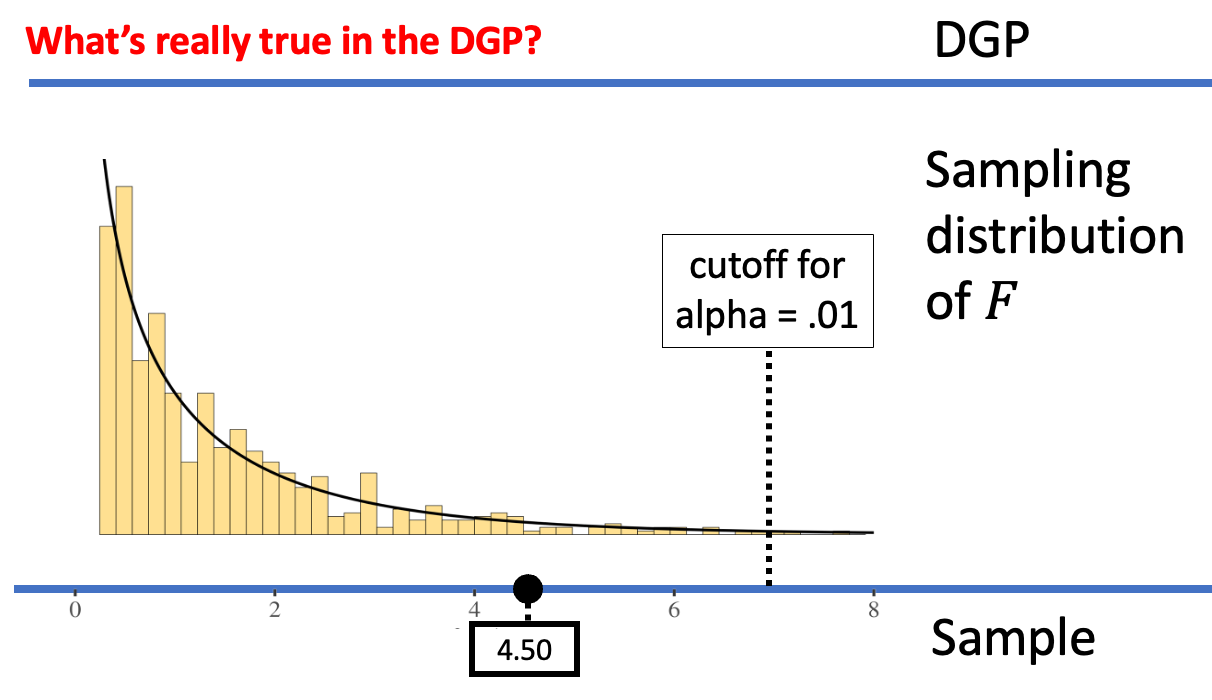
Because the sample F now falls below the .05 cutoff, we would decide to not reject the empty model. Whether we have made an error or not depends on what is really true in the DGP. If the empty model is true, then our decision to not reject it is the correct one. But if the empty model is not true, then we have made a Type II error.
Reducing the Chance of Error
We can reduce the chance of making a Type I error by making it harder to reject the empty model. We can accomplish this by moving the alpha criterion. For example, the figures below show what happens when we move the alpha criterion from .05 (left panel) to .01 (right panel).
|
|
When alpha = .05, the sample F was considered unlikely to have come from the empty model of the DGP. But when alpha = .01, the same sample F is not considered unlikely any more; it’s not out in the extreme tail. Whereas on the left we would reject the empty model, on the right, we would not reject the empty model. By making alpha = .01, we have made it harder to reject the empty model, and thus harder to make a Type I error (assuming the empty model is true).
If we want to avoid Type I error, the natural thing to do is to make alpha very small, which makes it very difficult to reject the empty model. But decreasing alpha actually increases the likelihood of making a Type II error. But if the empty model is not true we would actually want to reject the empty model. By not rejecting it when it is true, we have made a Type II error.
Summary of Type I and Type II Error
This is hard stuff to keep in your head. Don’t worry if you get confused; we still do too from time to time. To help, though, we’ve created a table that summarizes the concepts of Type I and Type II error.
| Model We Adopt Based on Data | What’s Really True | |
|---|---|---|
| Empty Model (\(\beta_1 = 0\)) | Complex Model (\(\beta_1 \neq 0\)) | |
| Empty Model | Yay us! | Type II Error |
| Complex Model (Reject Empty Model) | Type I Error | Yay us! |