Course Outline
-
segmentGetting Started (Don't Skip This Part)
-
segmentStatistics and Data Science: A Modeling Approach
-
segmentPART I: EXPLORING VARIATION
-
segmentChapter 1 - Welcome to Statistics: A Modeling Approach
-
segmentChapter 2 - Understanding Data
-
segmentChapter 3 - Examining Distributions
-
segmentChapter 4 - Explaining Variation
-
segmentPART II: MODELING VARIATION
-
segmentChapter 5 - A Simple Model
-
segmentChapter 6 - Quantifying Error
-
6.6 Interpreting and Using Z-Scores
-
segmentChapter 7 - Adding an Explanatory Variable to the Model
-
segmentChapter 8 - Digging Deeper into Group Models
-
segmentChapter 9 - Models with a Quantitative Explanatory Variable
-
segmentPART III: EVALUATING MODELS
-
segmentChapter 10 - The Logic of Inference
-
segmentChapter 11 - Model Comparison with F
-
segmentChapter 12 - Parameter Estimation and Confidence Intervals
-
segmentFinishing Up (Don't Skip This Part!)
-
segmentResources
list High School / Advanced Statistics and Data Science I (ABC)
6.6 Interpreting and Using Z-Scores
How Z-Scores Are Different From Standard Deviation
Standard deviation (SD) is roughly the average deviation of all scores from the mean. It can be seen as an indicator of the spread of the distribution. A z-score uses SD as a sort of ruler for measuring how far an individual score is above or below the mean.
A z-score tells you how many standard deviations a score is from the mean of its distribution, but doesn’t tell you what the standard deviation is (or what the mean is). Another way to think about it is that a z-score is a way of comparing a deviation of a score (the numerator) to the standard deviation of the distribution (the denominator).
Let’s use z-scores to help us make sense of our Thumb data. Calculate the z-score for a 65.1 mm thumb.
require(coursekata)
# this saves the mean and standard deviation of Thumb
mean <- mean(Fingers$Thumb)
sd <- sd(Fingers$Thumb)
# write code to calculate the z-score for a 65.1 mm Thumb
mean <- mean(Fingers$Thumb)
sd <- sd(Fingers$Thumb)
(65.1 - mean) / sd
ex() %>% {
check_output_expr(., "(65.1 - mean) / sd")
}0.572534942855165A single z-score tells us how many standard deviations away this particular 65.1 mm thumb is from the mean. Because the standard deviation is roughly the average distance of all scores from the mean, it is likely that most scores are clustered between one standard deviation above and one standard deviation below the mean. It is less likely to find scores that are two or three standard deviations away from the mean. Z-scores give us a way to characterize scores in a bit finer way than just bigger or smaller than the mean.
Using Z-Scores to Compare Scores From Different Distributions
One more use for the z-score is to compare scores that come from different distributions, even if the variables are measured on different scales.
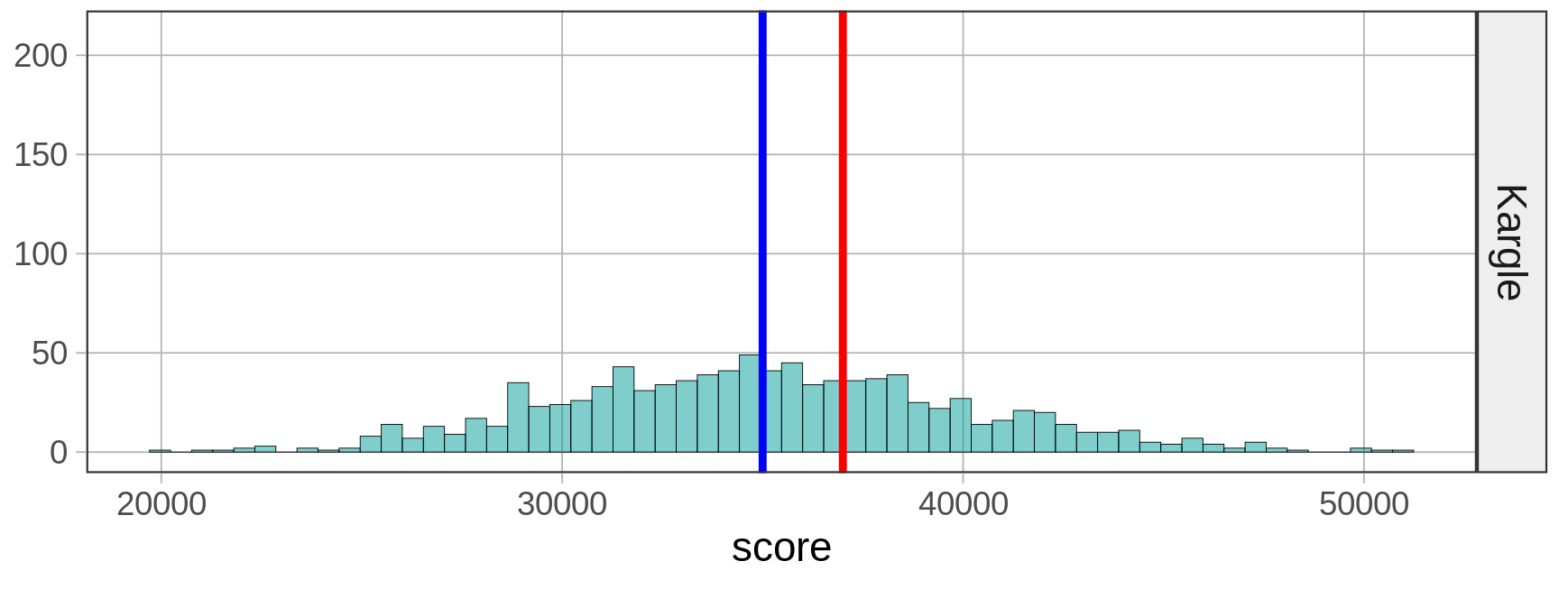
Here’s the distribution of scores for all players of the video game Kargle again. We know that the distribution is roughly normal, the mean score is 35,000, and the standard deviation is 5,000.
Her z-score is +2. Wow, two standard deviations from the mean! Not a lot of scores are way up there.
Now let’s say you have another friend who doesn’t play Kargle at all. She plays a similar game, though—Spargle! Spargle may be similar, but it has a completely different scoring system. Although the scores on Spargle are roughly normally distributed, their mean is 50, and the standard deviation is 5. This other friend has a high score of 65 on Spargle.
Now: what if we want to know which friend, in general, is a better gamer? The one who plays Kargle, or the one who plays Spargle? This is a hard question, and there are lots of ways to answer it. The z-score provides one way.
We’ve summarized the z-scores for your two friends in the table below.
| Player | Player Score | Game Mean | Game SD | Player Z-Score |
| Kargle Player | 45,000 | 35,000 | 5,000 | +2.0 |
| Spargle Player | 65 | 50 | 5 | +3.0 |
Looking at the z-scores helps us to compare the abilities of these two players, even though they play games with different scoring systems. Based on the z-scores, we could say that the Spargle player is a better gamer, because she scored three standard deviations above the mean, compared with only two standard deviations above the mean for the Kargle player.
Of course, nothing is really definite with such comparisons. Someone might argue that Spargle is a much easier game, and so the people who play it tend to be novices. Maybe the Kargle player is better, because even though her z-score is lower, she is being compared to a more awesome group of gamers!