12.4 Interpreting the Confidence Interval

Now that we have spent some time constructing confidence intervals, it is important to pause and think about what a confidence interval means, and how it fits with other concepts we have studied so far.

Confidence Intervals Are About the DGP

One common misconception about confidence intervals is that they define lower and upper cutoffs for where .95 of the $b_1$s might fall (see the left part in the figure below). We can forgive you if you are thinking this, because we did just spend time calculating a confidence interval by centering a sampling distribution at the sample $b_1$, and then finding the values of $b_1$ that would fall beyond the two .025 cutoffs.

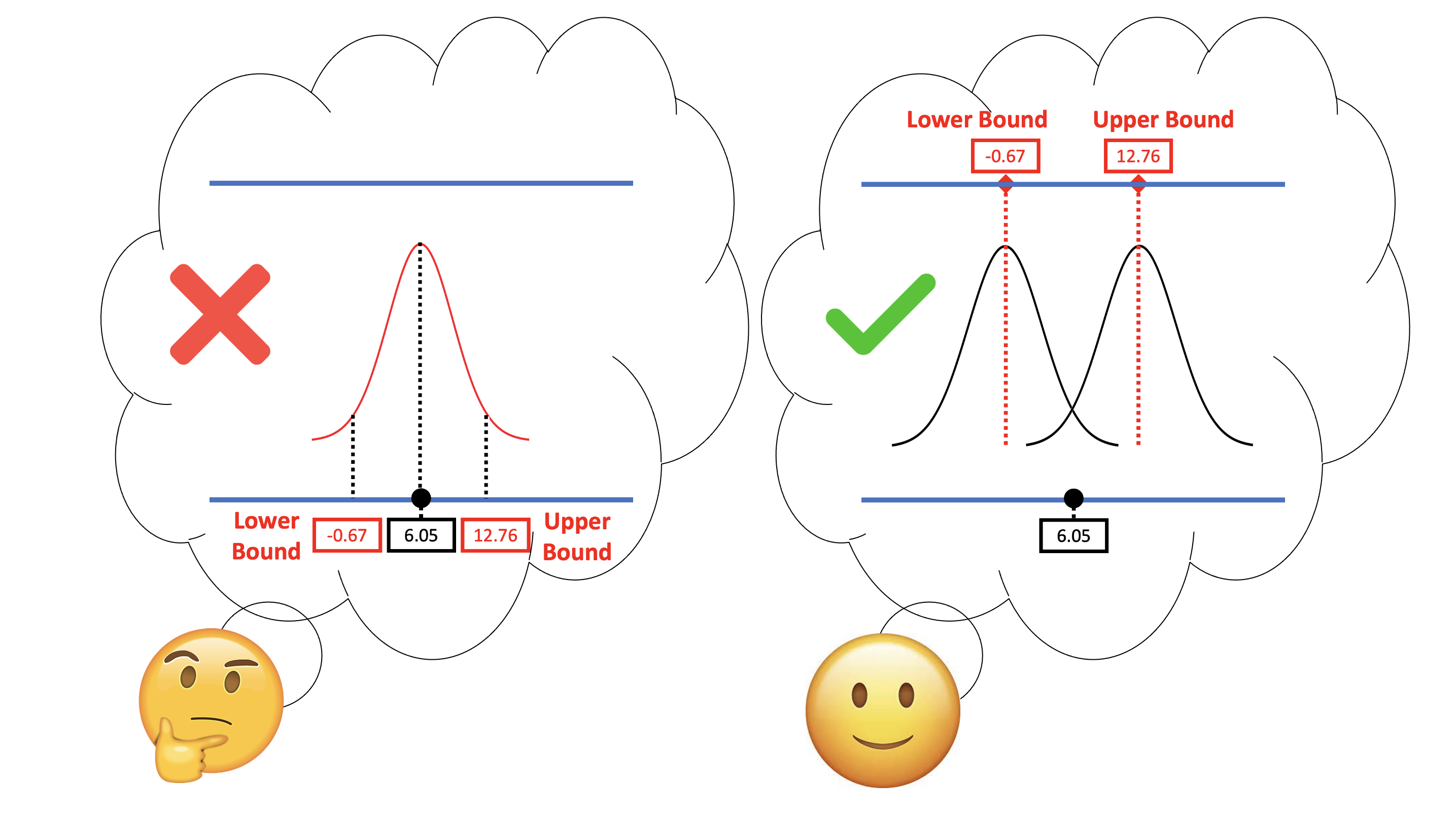
But that was just a method for calculating the interval, not a definition of what the interval actually refers to. It is important to remember that the concept of confidence interval was developed by mentally moving the sampling distribution of $b_1$s up and down the scale of ${\beta }_1$, considering the alternative values of ${\beta }_1$ in the DGP that could, with 95% likelihood, have produced the sample $b_1$ found by the researchers. (The right part of the picture above will remind you of this way of thinking.)

If we did want to know the range of possible sample $b_1$s that are likely in the world, we would actually need to know the true ${\beta }_1$ in the DGP. But we don’t know this. This is why we have to hypothesize lots of different values of ${\beta }_1$ by sliding the sampling distribution around. Each ${\beta }_1$ generates a different range of likely $b_1$s.

Error in an Estimate

The $b_1$ observed by the researchers is the best estimate of what the true ${\beta }_1$ might be. This estimate is often referred to as a point estimate. Based on the available data, which generally just comes from the current study, it is the best estimate the researchers can come up with for what the true ${\beta }_1$ is. There is no reason to guess higher or lower than this point estimate.

But being the best doesn’t mean it’s right. This estimate is almost certainly wrong. It might be too low or it might be too high, but we don’t know which way it is wrong. And to make matters worse, it’s hard to tell whether the estimate is correct or not, or how far off it is from the true DGP, because we don’t really know what the true ${\beta }_1$ is.

The confidence interval provides us with a way of addressing this problem. It tells us how wrong we could be, or put another way, how much error there might be in our estimate.

If the confidence interval is relatively wide given the situation, as it is in the tipping study, we would be saying something like, “the estimated effect of adding a smiley face to the check is $6.05. But there is a lot of error in the estimate. The true effect could be as low as 0 or slightly below that, or as high as $13.”

The width of the confidence interval (CI) tells us what the true ${\beta }_1$ in the DGP might be. When the CI is narrower, we think our estimate is closer to the true ${\beta }_1$ than when the CI is wider.

It is important to note that when we talk about the error in an estimate we are using the term error to mean something a little different than we have learned up to now. Previously, when we developed the concept of error (as in DATA = MODEL + ERROR), we were referring to the gap between the predicted tip for each table based on a model, and the actual tip left by that table. The errors were the individual residuals for each table.

When we think about error around a parameter estimate though, we’re not thinking about individual tables any more. A single table can’t have a $b_1$! A single table can’t have an average difference between control and smiley face tables. The idea of $b_1$ only exists at the level of a whole sample. Error in $b_1$, therefore, means how different the sample estimate is from the true ${\beta }_1$ in the DGP.

Because we generally don’t know what the true ${\beta }_1$ is, we can’t know how far the estimate is from the true ${\beta }_1$. But because we have a sampling distribution, we can know how much the estimate might vary across samples given a particular DGP, and based on that, how much variation or error there might be in the range of possible ${\beta }_1$s that could have produced the sample estimate.

In the case of the tipping experiment, we started with a point estimate of the ${\beta }_1$ parameter ($6.05) – the effect of having a smiley face on a table’s tip. The confidence interval is not telling us about the range of tips provided by all the tables in the study, but about the range of possible ${\beta }_1$s that could have generated our particular $b_1$. In other words, it tells us how wrong our point estimate might be.

What Does the 95% Mean?

One question you might have is this: what does it mean to have 95% confidence?

Let’s start by explaining what it does not mean. It does not mean that there is a .95 probability that the true ${\beta }_1$ falls within the confidence interval. This is a confusing point, and one statisticians care a lot about. If you say there’s a 95% chance that the true parameter falls in this range, they will correct you.

One reason they will correct you is that ${\beta }_1$ either is in this range (100%) or is not in this range (0%). You don’t know what ${\beta }_1$ is so you can’t tell if the probability is 100% or 0% but it’s definitely not a 95% probability. What is uncertain is your knowledge (measured in confidence rather than probability).

The other reason they will correct you is that there isn’t actually a .95 chance that the ${\beta }_1$ is in a certain range if the sample $b_1=6.05$, but rather a .95 chance of getting the observed sample $b_1$ if the ${\beta }_1$ is within a certain range. In probability theory, the probability of A given B is not the same as the probability of B given A, which is another way of saying the probability of B if A is true. (This is related to Bayes’ Rule, something you might want to dig deeper into, but we won’t do that here.)

Because of this issue, someone (actually, a mathematician named Jerzy Neyman, in 1937) came up with the idea of saying “95% confident” instead of “95% probable.” Our guess is that all the statisticians and mathematicians breathed a sigh of relief over this.

When you construct a 95% confidence interval, therefore, you are saying that you are 95% confident (alpha = .05) that the true ${\beta }_1$ in the DGP falls within the interval. You can’t have a 100% confidence interval, by the way, because the probability model we use for the sampling distribution – the t-distribution – has tails that never really touch 0 on the y-axis. Because of this, we can’t really define the point at which the probability of Type I error would be equal to 0.

Confidence Intervals and Model Comparison

We have now used the sampling distribution of $b_1$ for two purposes: deciding whether or not to reject the empty model (or null hypothesis); and constructing a confidence interval. Now let’s think just a bit about how these two uses fit together.

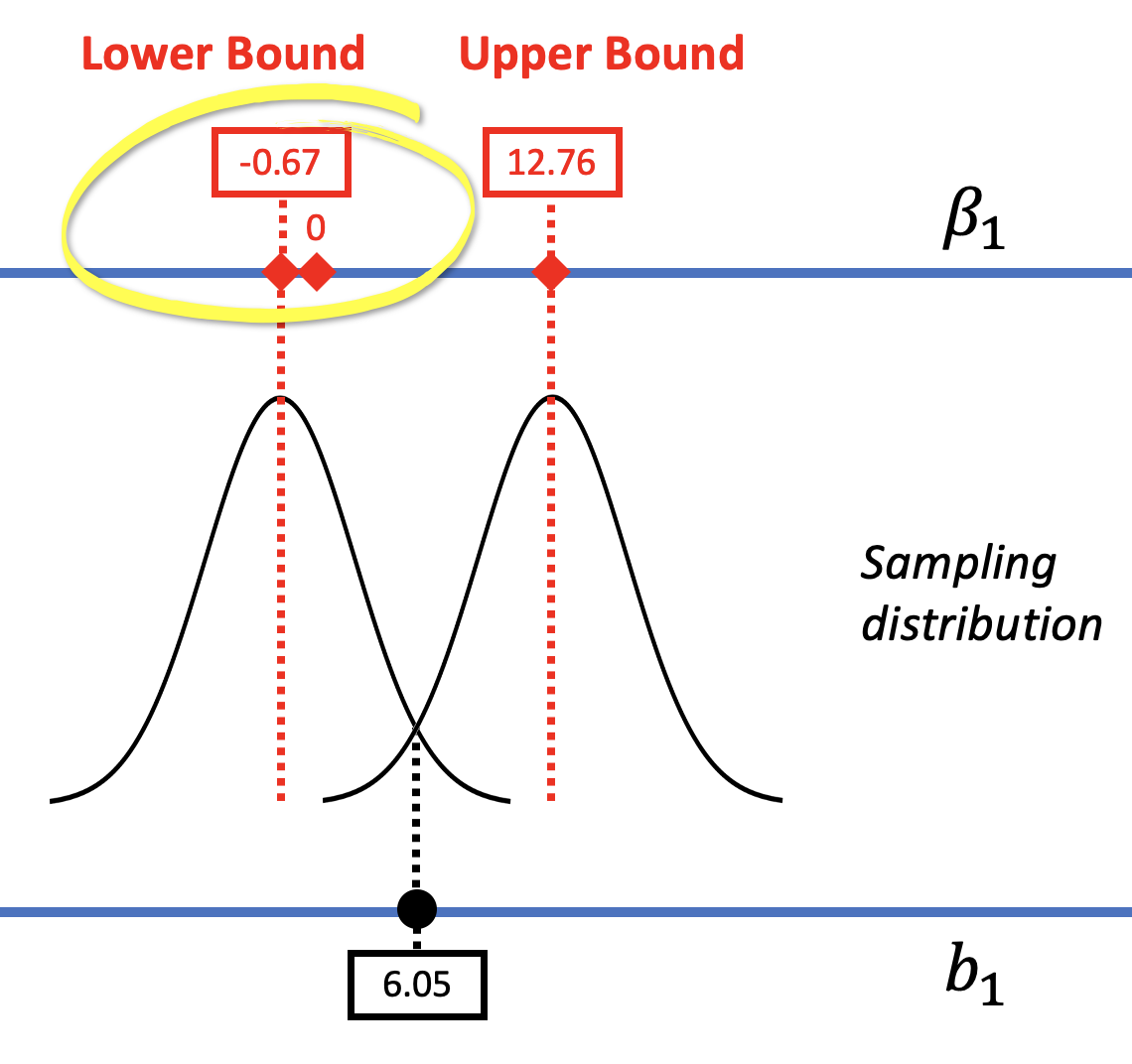
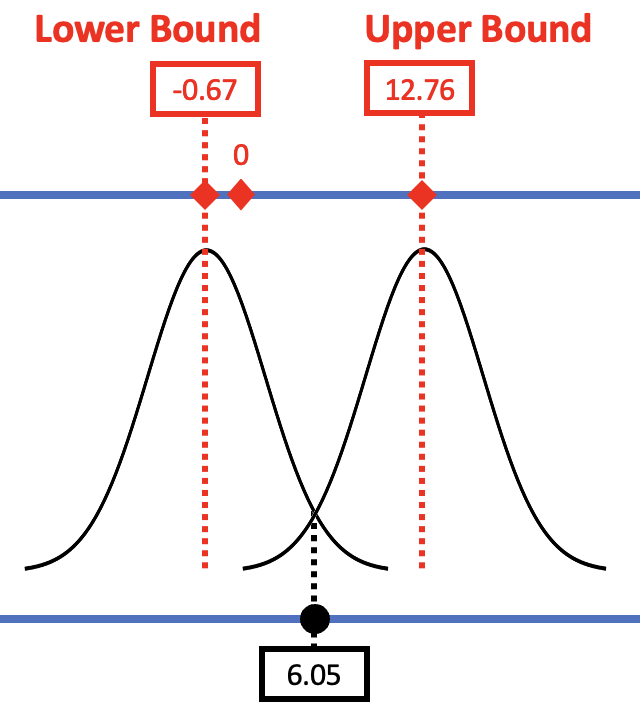
The confidence interval provides us with a range of models of the DGP (i.e., a range of possible ${\beta }_1$s) that we would not reject. In the case of the tipping study, we can be 95% confident that the true effect of smiley faces on tips in the DGP lies somewhere between -.67 and 12.76.

We would reject any values of ${\beta }_1$ that do not fall within our confidence interval. In this case, 0 happens to fall within the confidence interval (see the left panel in the figure below) and so we do not rule it out as a possible model of the DGP.

Using A Confidence Interval to Evaluate the Empty Model	Using a Hypothesis Test to Evaluate the Empty Model

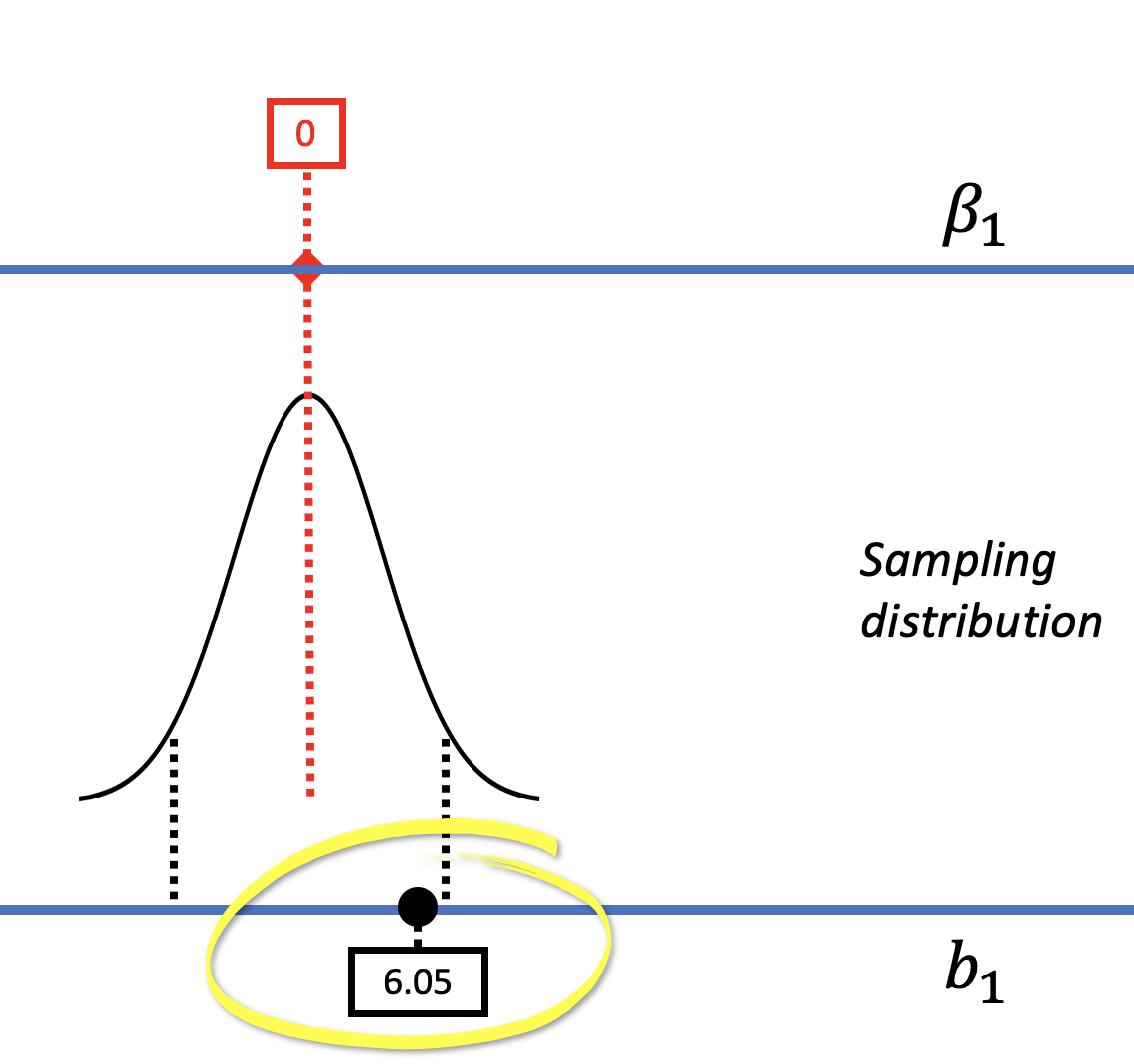
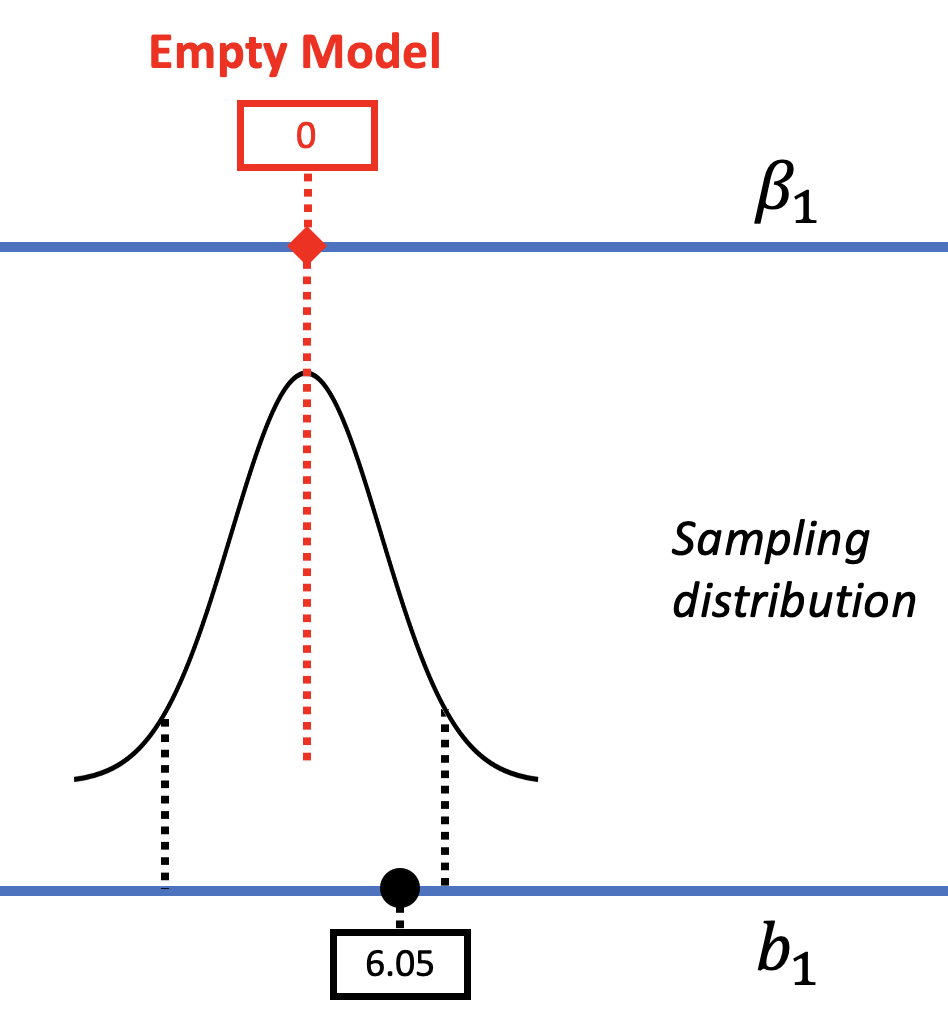
In the right panel of the figure above, the model comparison (or hypothesis testing) approach considers just one particular model of the DGP, not a range of models. In this model, in which ${\beta }_1=0$ (also called the empty model or null hypothesis), there is no effect of smiley face in the DGP. We used shuffle() to mimic such a DGP, and built a sampling distribution centered at 0. We can see in the picture above that if such a DGP were true, our sample $b_1$ would not be unlikely.

We then used the sampling distribution as a probability distribution to calculate the probability of getting a sample $b_1$ of $6.05 or more extreme, whether positive or negative, if the empty model were true (i.e., the p-value). Based on the p-value of .08, we decided to not reject the empty model, .08 being slightly higher than the .05 cutoff we had set as our alpha criterion.

These two approaches – null hypothesis testing and confidence intervals – both provide ways of evaluating the empty model, and both lead us to the same conclusion in the tipping study: the empty model, where ${\beta }_1=0$, cannot be ruled out as a possible model of the DGP.

If the 95% confidence interval does not include 0, then we would reject the empty model because we are not confident that ${\beta }_1=0$. And if the confidence interval does not include 0, the p-value for the null hypothesis test would be less than .05, again leading us to reject the empty model. This is not just a coincidence. The two approaches will always corroborate each other because both are based on the same underlying logic and the same sampling distributions (i.e., with the same shape and spread).

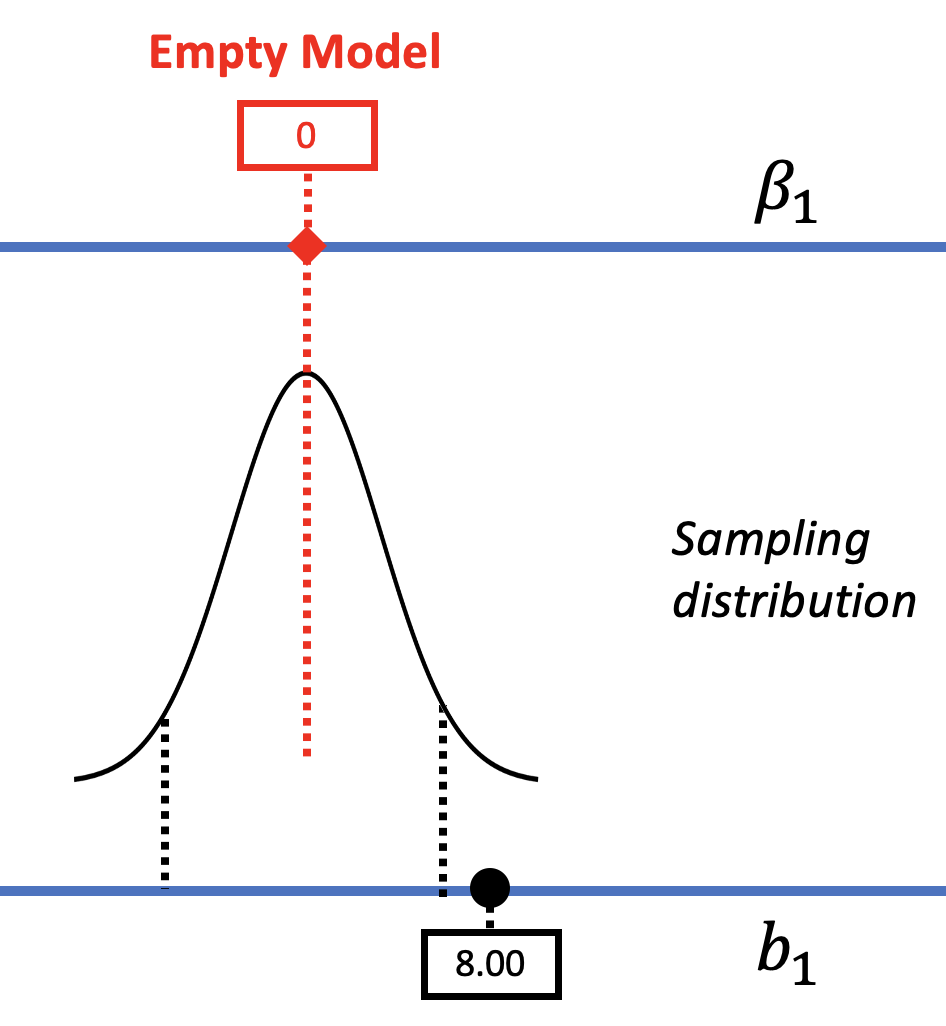
As another example, let’s consider a second tipping study done by another team of researchers. They got very similar results but this time, their $b_1$ was $8 (see right panel of figure below), instead of $6.05 (pictured in the left panel). Their standard error (and margin of error) was the same as in the original study. The figure below represents the results of the two studies in the context of a sampling distribution from a DGP where ${\beta }_1=0$.

Original Study ($b_1=6.05$)	Second Study ($b_1=8.00$)

We don’t really believe that the DGP has changed, so we wouldn’t say the ${\beta }_1$ has changed for this study. But everything else would change – the best estimate of ${\beta }_1$, the p-value, and the confidence intervals. The p-value will be lower because the $b_1$ would now be in the unlikely tails if the empty model were true in the DGP.

Let’s take a look at how the confidence interval might be different across these two studies.

Original Study ($b_1=6.05$)	Second Study ($b_1=8.00$)

In the left panel of the figure the confidence interval (marked by the two red boxes) is centered around an assumed ${\beta }_1$ that is the same as the observed $b_1$ (6.05), and 0 is just inside the confidence interval. In this study, we did not reject the empty model as a model of the DGP because it was one of the values included in the 95% confidence about.

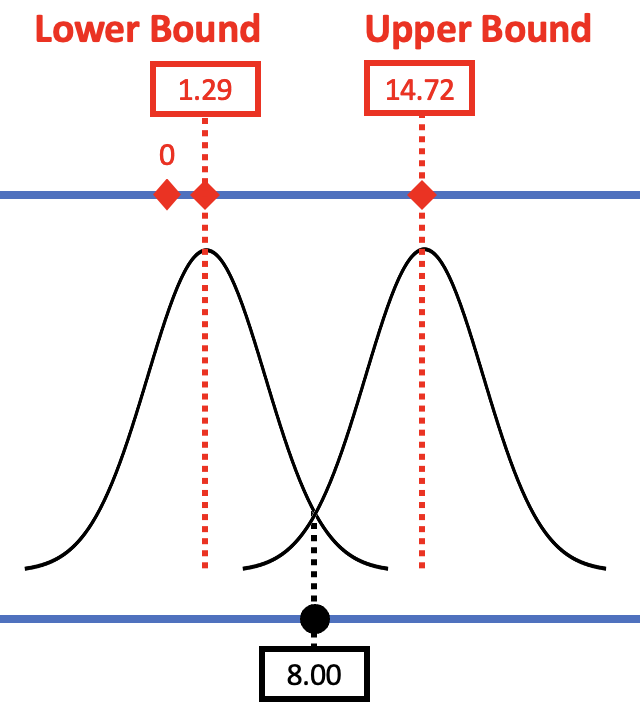
In the right panel of the figure, we see what happened in the second study where the observed $b_1$ was a little higher (8.00). The new confidence interval is centered at 8.00, and 0 is now outside the confidence interval. Based on the results of this second study, we would reject the empty model as a model of the DGP.

It is also worth noting that we get a lot more information from the confidence interval than we do from the p-value. For example, in the original tipping study (where $b_1=6.05$), even when we don’t reject the null hypothesis (0), we would not want to therefore accept it and claim that 0 is the true value of ${\beta }_1$. We can see from the confidence interval that even though the true value of ${\beta }_1$ in the DGP might be 0, there are many other values it also might be. Confidence intervals help us to remember this fact.