11.3 The Sampling Distribution of F

Using the Sampling Distribution of F

Having constructed a sampling distribution of F, let’s use it to evaluate the empty model of Tip. Our approach will be similar to the one we used in the previous chapter based on the sampling distribution of \(b_1\). We first construct a sampling distribution of F assuming the empty model is true (e.g., with shuffle()), and then look to see how likely the sample F would be to have occurred by chance if the empty model were true.

Because the sampling distribution of F clearly has a different shape than the sampling distribution of \(b_1\), however, we will need to adjust our method for judging likelihood.

Samples with extremely high Fs (e.g., an F of 8 or 12) are unlikely to be generated from a random DGP. But low sample Fs are quite common from a purely random DGP. Only high values of F – those in the upper tail – would make us doubt that the empty model produced our data.

With the sampling distribution of F, we only need to look at one tail of the distribution. We know that the F ratio can never be less than 0. We just want to know how likely it is to get an F as high as the one we observed.

We can use a function called lower() to fill the lower .95 of a sampling distribution in a different color than the upper .05 tail by adding this argument to a histogram: fill = ~lower(fVal, .95). Try adding this argument to the sampling distribution in the code window below.

We used a similar function called middle() before and there’s a related upper() function as well.

Interpreting the Sample F from the Tipping Experiment

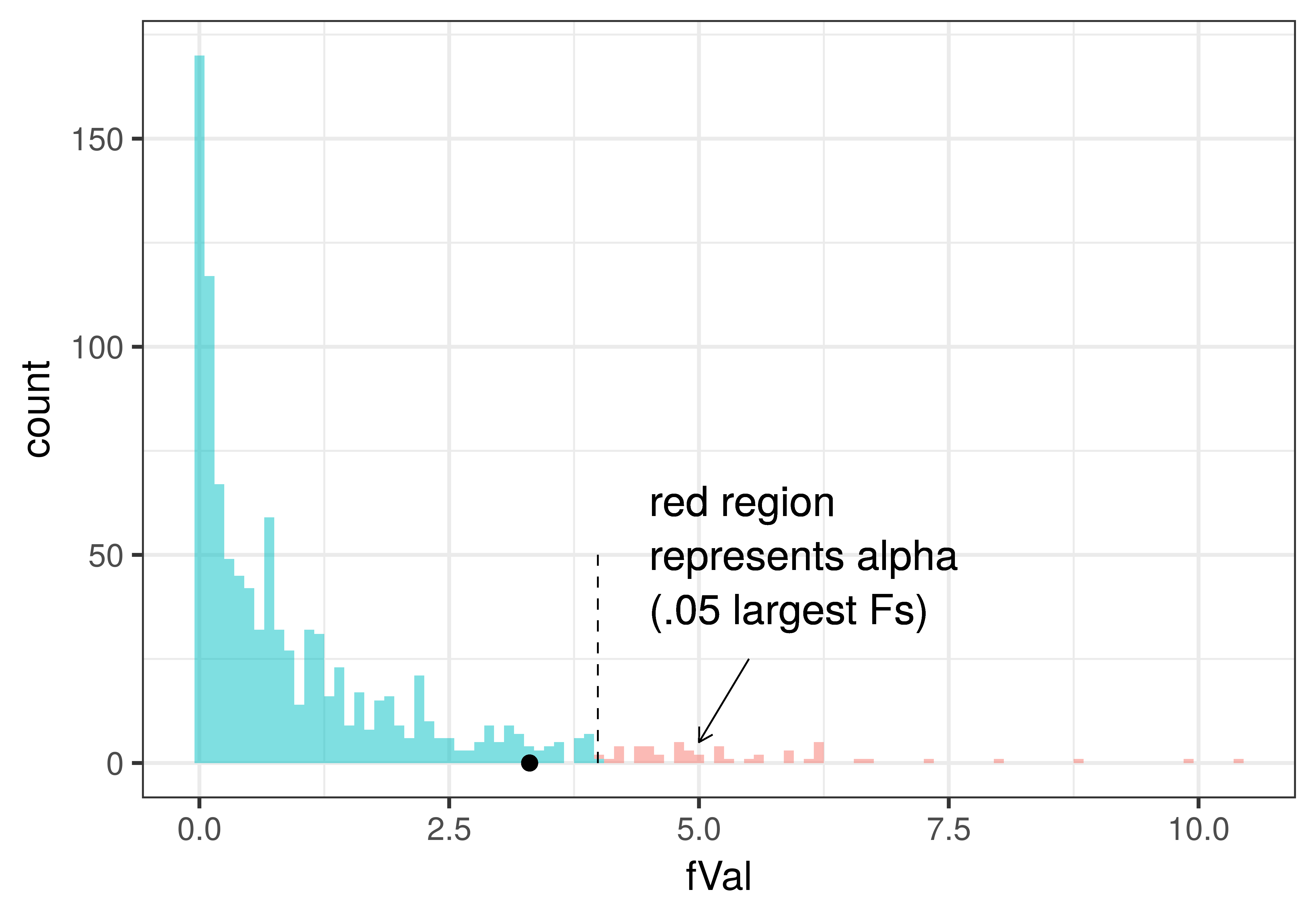
In the plot below we have added a dotted line to show the alpha criterion (the point that divides the unlikely Fs (i.e., .05 of the largest Fs generated by the empty model, which are colored red) from those considered not unlikely . We also have added in a black point to show where the sample F from the tipping experiment was. Because the sample F falls in the not unlikely region of the sampling distribution, we would probably decide to not reject the empty model based on the results of the experiment.

We can color the same plot a little differently to represent the p-value for the actual F found in the tipping experiment. In the plot below, p-value is represented in purple: all the randomly generated Fs from the empty model that were greater than or equal to the observed sample F of 3.30. For reference we have left in the dashed line to show the alpha criterion of .05.

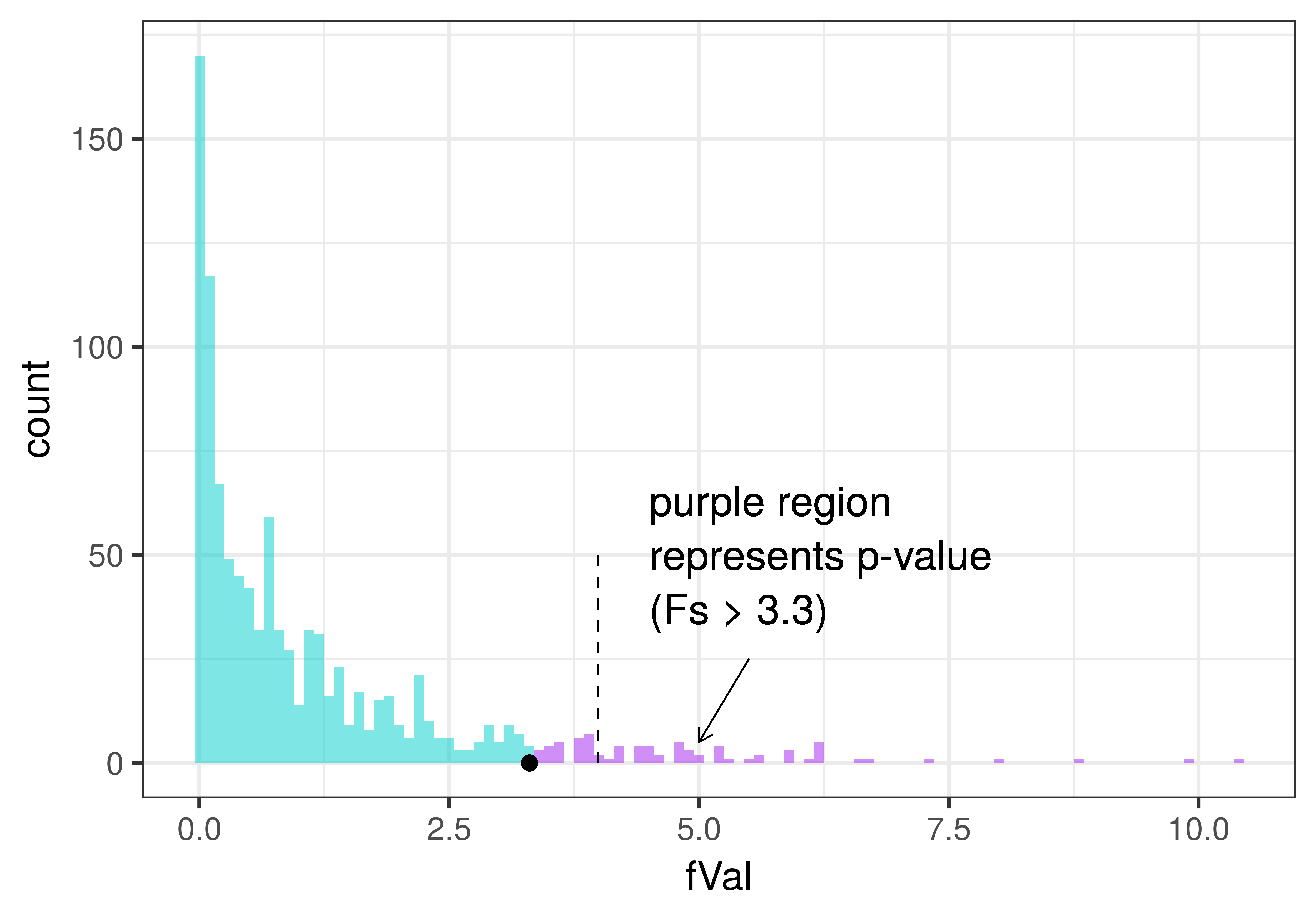
We can see from the plot that the p-value (purple area) will be greater than .05 (represented by the dashed line), which is another way of saying that the observed F is not in the unlikely region of the sampling distribution.

Calculating P-Value from the Sampling Distribution of F

To calculate the exact p-value, we can use the tally() function, using the proportion of our 1000 simulated Fs as extreme or more extreme than the observed F, to estimate of the probability of generating such an F if the empty model is true.

fVal > sample_F
 TRUE FALSE 
0.081 0.919

The resulting p-value (about .08) is larger than the alpha criterion of .05, meaning that the sample F is not in the the region we have defined as unlikely. (Note that your estimate of p-value may be a little different from ours because each is based on a different set of 1000 randomly generated Fs.)

Based on this p-value, we would probably not reject the empty model of Tip. It’s possible that even if the empty model is true (that is, \(\beta_1 = 0\) and \(\text{PRE} = 0\)), we still might have observed an F just by random chance as high as the one actually observed (3.30)

P-Value Calculated from Sampling Distribution of \(b_1\) versus F

In the prior chapter we pointed out that the p-value for the effect of Condition in the tipping experiment could also be found in the ANOVA table produced by the supernova() function. Here it is again.

supernova(lm(Tip ~ Condition, data = TipExperiment))

Analysis of Variance Table (Type III SS)
Model: Tip ~ Condition

                              SS df      MS     F    PRE     p
----- ----------------- -------- -- ------- ----- ------ -----
Model (error reduced) |  402.023  1 402.023 3.305 0.0729 .0762
Error (from model)    | 5108.955 42 121.642                   
----- ----------------- -------- -- ------- ----- ------ -----
Total (empty model)   | 5510.977 43 128.162                   

Notice that the p-value of .0762 is close to the p-value we just calculated using the sampling distribution of F, and also is close to the p-value we obtained in the previous chapter using the sampling distribution of \(b_1\). This is not an accident. The reason these p-values are similar is because they are testing the same thing – the effect of smiley face on Tip – using different methods.

We have now used shuffle() to construct sampling distributions for three sample statistics: \(b_1\), PRE, and F. By using shuffle(), we were simulating a DGP in which the empty model is true, i.e., that whether or not a smiley face is drawn on the check does not affect how much a table tips. The variation we see in the sampling distributions is assumed to be due to random sampling variation.

The shapes of the sampling distributions are different for \(b_1\) than for F (see figure below). The sampling distribution of \(b_1\) is roughly normal in shape, while the one for F has a distinctly asymmetric shape, with a long tail off to the right. The rejection region defined by alpha is split between two tails for the sampling distribution of \(b_1\), but is all in the upper tail of the sampling distribution of F.

Once we constructed the sampling distribution, we used it to put the observed sample statistic in context. Specifically, it enabled us to ask how likely it would be to select a sample with a sample statistic – be it \(b_1\), PRE, or F – as extreme or more extreme as the statistic observed in the sample. The answer to this question is the p-value.

The p-value is the probability of getting a parameter estimate as extreme or more extreme than the sample estimate given the assumption that the empty model is true. The p-value is calculated based on the sampling distribution of the parameter estimate under the empty model.

We can use the p-value to decide, based on our stated alpha of .05, whether the observed sample statistic would be unlikely or not if the empty model is true. If we judge it to be unlikely (i.e., p < .05), then we would most likely decide to reject the empty model in favor of the more complex model. But if the p-value is greater than .05, which it is for the Condition model of Tip, we would probably decide to stick with the empty model for now, pending further evidence.