Course Outline
-
segmentGetting Started (Don't Skip This Part)
-
segmentStatistics and Data Science: A Modeling Approach
-
segmentPART I: EXPLORING VARIATION
-
segmentChapter 1 - Welcome to Statistics: A Modeling Approach
-
segmentChapter 2 - Understanding Data
-
segmentChapter 3 - Examining Distributions
-
segmentChapter 4 - Explaining Variation
-
segmentPART II: MODELING VARIATION
-
segmentChapter 5 - A Simple Model
-
segmentChapter 6 - Quantifying Error
-
segmentChapter 7 - Adding an Explanatory Variable to the Model
-
segmentChapter 8 - Digging Deeper into Group Models
-
segmentChapter 9 - Models with a Quantitative Explanatory Variable
-
9.7 Assessing Model Fit with PRE and F
-
segmentPART III: EVALUATING MODELS
-
segmentChapter 10 - The Logic of Inference
-
segmentChapter 11 - Model Comparison with F
-
segmentChapter 12 - Parameter Estimation and Confidence Intervals
-
segmentChapter 13 - What You Have Learned
-
segmentFinishing Up (Don't Skip This Part!)
-
segmentResources
list High School / Advanced Statistics and Data Science I (ABC)
9.7 Assessing Model Fit with PRE and F
Comparing PRE for the Two Models
Let’s go back to the ANOVA tables for the Height2Group and Height models.
Height2Group Model
Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height2Group
SS df MS F PRE p
----- --------------- | --------- --- ------- ------ ------ -----
Model (error reduced) | 830.880 1 830.880 11.656 0.0699 .0008
Error (from model) | 11049.331 155 71.286
----- --------------- | --------- --- ------- ------ ------ -----
Total (empty model) | 11880.211 156 76.155 Height Model
Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height
SS df MS F PRE p
----- --------------- | --------- --- -------- ------ ------ -----
Model (error reduced) | 1816.862 1 1816.862 27.984 0.1529 .0000
Error (from model) | 10063.349 155 64.925
----- --------------- | --------- --- -------- ------ ------ -----
Total (empty model) | 11880.211 156 76.155 PRE has the same interpretation in the context of regression models as it does for the group models. As we have pointed out, the total sum of squares is the same for both models. And the PRE is obtained in both cases by dividing SS Model by SS Total.
Many statistics textbooks emphasize the difference between ANOVA models (such as our two- and three-group models) and regression models (such as our height model). But in fact, the two types of models are fundamentally the same and easily incorporated into the General Linear Model framework. In the context of regression, PRE is sometimes referred to as \(R^2\) (R-squared).
For the models we are considering, no matter what you call it, the interpretation of PRE is identical: it is the proportion of error reduced by the complex model compared with the empty model. Or, put another way, the proportion of variation explained by the model.
Using the F Ratio for Comparing Models
Finally, we can also assess model fit by looking at the F ratio, which we introduced in a previous chapter. Whereas PRE is a proportion based on sums of squares, the F statistic is a ratio of two variances (also called mean squares or MS), obtained by dividing SS by df. The numerator is the MS Model, which indicates the amount of variation explained by the model per degree of freedom spent; and the denominator is MS Error, which indicates the amount of variation left unexplained by the model per degree of freedom remaining.
More on F Versus PRE
To get a more concrete idea of why this matters, let’s compare yet another group model to the Height model: the Height10Group model. The following R code creates a new grouping variable called Height10Group (inside the Fingers data frame), which divides the sample into 10 equally-sized groups based on Height, and then makes it a factor.
Fingers$Height10Group <- ntile(Fingers$Height, 10)
Fingers$Height10Group <- factor(Fingers$Height10Group)We fit a group model of Thumb using Height10Group, and placed it on the jitter plot of the 10 groups. The model’s predictions are shown as 10 horizontal line segments, each representing the mean of each group.
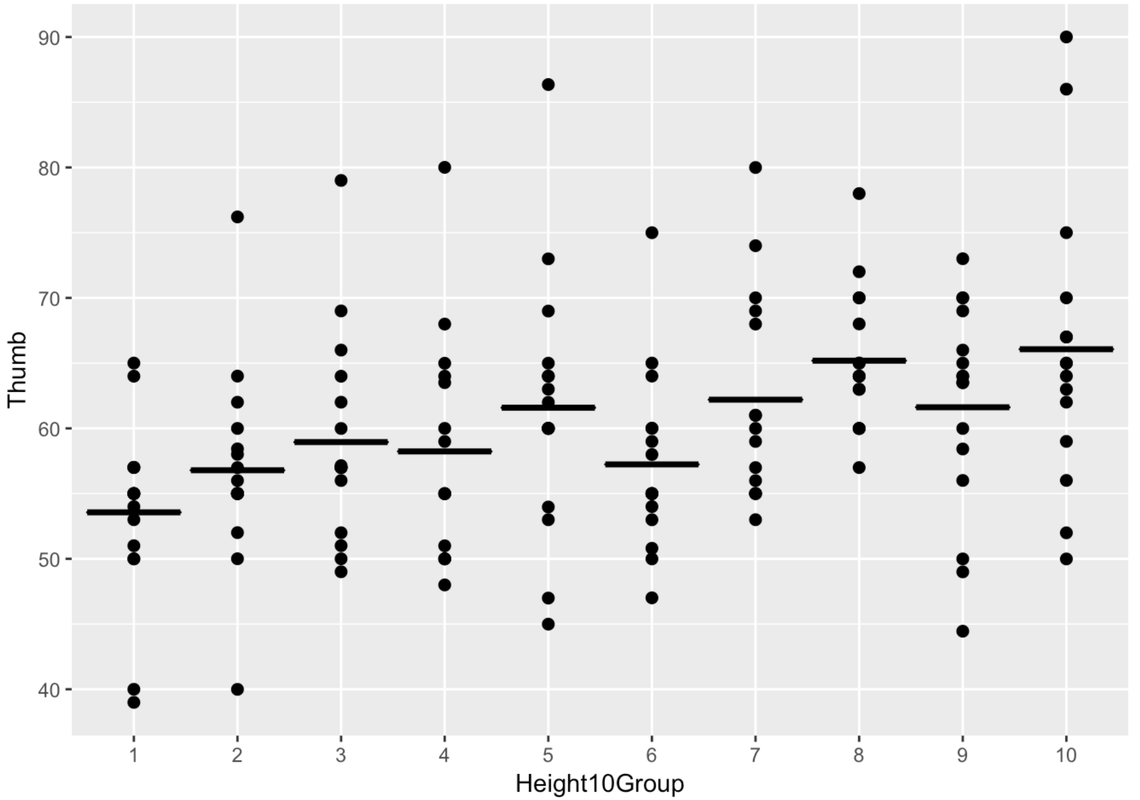
Here’s the code used to fit a model of Thumb using Height10Group, and produce the ANOVA table.
Height10Group_model <- lm(Thumb ~ Height10Group, data = Fingers)
supernova(Height10Group_model)Below are the supernova() tables for three models: Height2Group, Height10Group, and Height. The outcome variable for all three models, again, is Thumb.
Height2Group Model
Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height2Group
SS df MS F PRE p
----- --------------- | --------- --- ------- ------ ------ -----
Model (error reduced) | 830.880 1 830.880 11.656 0.0699 .0008
Error (from model) | 11049.331 155 71.286
----- --------------- | --------- --- ------- ------ ------ -----
Total (empty model) | 11880.211 156 76.155 Height10Group Model
Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height10Group
SS df MS F PRE p
----- --------------- | --------- --- ------- ----- ------ -----
Model (error reduced) | 1920.474 9 213.386 3.149 0.1617 .0017
Error (from model) | 9959.737 147 67.753
----- --------------- | --------- --- ------- ----- ------ -----
Total (empty model) | 11880.211 156 76.155 Height Model
Analysis of Variance Table (Type III SS)
Model: Thumb ~ Height
SS df MS F PRE p
----- --------------- | --------- --- -------- ------ ------ -----
Model (error reduced) | 1816.862 1 1816.862 27.984 0.1529 .0000
Error (from model) | 10063.349 155 64.925
----- --------------- | --------- --- -------- ------ ------ -----
Total (empty model) | 11880.211 156 76.155 To see how many degrees of freedom are used by a model, look at the df column in the row that says “Model (error reduced).” Notice that the Height10Group model costs us nine degrees of freedom, eight more than either the Height2Group model or the Height model (they each just spend one).
What do we get for these extra degrees of freedom? When we go from the Height2Group model to the Height model, PRE goes up from .07 to .15 without spending any additional degrees of freedom. That seems like a no brainer!
The Height10Group model produces the highest PRE of all the models (.16), but it costs us eight additional degrees of freedom. A model that predicts 10 different group means is not very elegant compared to one with just a y-intercept and slope. Here’s what the Height10Group model would look like in GLM notation:
\(Y_i=b_0+b_1X_{1i}+b_2X_{2i}+b_3X_{3i}+b_4X_{4i}+\)\(b_5X_{5i}+b_6X_{6i}+b_7X_{7i}+b_8X_{8i}+b_9X_{9i}+e_i\)
Compare that jumble of symbols with the Height model:
\[b_0+b_1X_i\]
That’s a truly elegant model! True, it doesn’t reduce error quite as much as the Height10Group model. But the regression model has a PRE of .15 with just two parameters (\(b_0\) and \(b_1\)) while the 10 group model estimates 8 more parameters (\(b_2\) to \(b_9\)) to get to a PRE of just .16. Elegant models add a lot of explanatory power without estimating a lot of parameters unnecessarily.
Comparing F Ratios for the Three Models
The supernova() function also calculated the F ratio for each of the three models. As we can see from the table below, the F ratio paints a different picture of the three models than we get by looking only at PRE.
| Model (Group) | PRE | F Ratio |
|---|---|---|
| Height2Group Model | .0699 | 11.656 |
| Height10Group Model | .1617 | 3.149 |
| Height Model | .1529 | 27.984 |
Going by PRE alone, the Height10Group model would appear to be the best one. But when we use F, which incorporates degrees of freedom into our model comparison, the Height model is the clear winner, with an F of 27.984. The Height10Group model is by far the worst, with an F of 3.149.