8.5 Measures of Effect Size
Revisiting the Tipping Study
Back in Chapter 4 we learned about an experiment that investigated whether drawing smiley faces on the back of a check would cause restaurant servers to receive higher tips (Rind & Bordia, 1996).
The study was a randomized experiment. A female server in a particular restaurant was asked to either draw a smiley face on the check or not for each table she served following a predetermined random sequence. The outcome variable was the percentage tipped by each table (Tip).
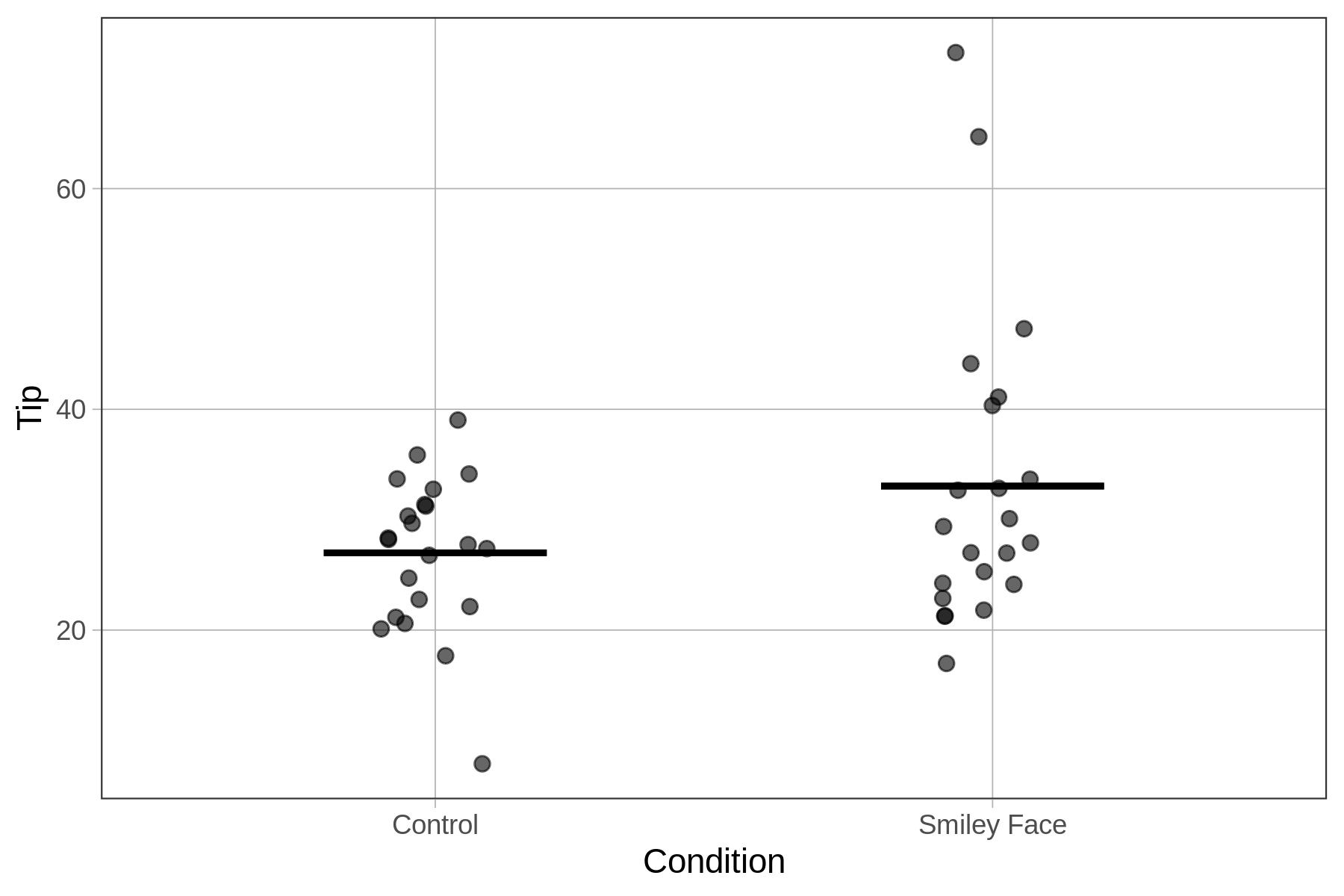
Distributions of tip percentages in the two groups (n=22 tables for each Condition) are shown below. We’ve also overlaid the best fitting model using gf_model().
Condition_model <- lm(Tip ~ Condition, data = TipExperiment)
gf_jitter(Tip ~ Condition, data = TipExperiment, width = .1) %>%
gf_model(Condition_model)
One question you might be asked about a statistical model is: How big is the effect? If you are modeling the effect of one variable on another (e.g., condition on tip percent), it’s natural for someone to ask this question.
This leads us to a discussion of effect size, and how to measure it. We haven’t used the term effect size up to now, but we have, in fact, presented two measures of effect size. Here we will review these two measures, and add a third.
Mean Difference (aka \(b_1\))
The most straightforward measure of effect size in the context of the two-group model is simply the actual difference in means between the two groups on the outcome variable.
These are the parameter estimates from the condition model of tip percent.
Call:
lm(formula = Tip ~ Condition, data = TipExperiment)
Coefficients:
(Intercept) ConditionSmiley Face
27.000 6.045 In the TipExperiment data set we can see that the size of the condition effect is about 6 percentage points: tables that got smiley faces on their checks tip an additional 6 percent of their check, on average, compared with tables that didn’t get the smiley face.
R: The b1() Function
The parameter estimates in the question above came from running lm(Tip ~ Condition, data = TipExperiment). Another, more direct, way to find the \(b_1\) estimate (in this case the mean difference between the two groups) is to use the b1() function (part of the supernova R package). Change the function from lm() to b1() in the window below to see how this works.
require(coursekata)
# change the function
lm(Tip ~ Condition, data = TipExperiment)
b1(Tip ~ Condition, data = TipExperiment)
ex() %>% check_or(
check_function(., "b1") %>%
check_result() %>%
check_equal,
override_solution(., 'b0(Tip ~ Condition, data = TipExperiment)') %>%
check_function("b0") %>%
check_result() %>%
check_equal()
)Note that when you run the b1() function on the Condition model it returns 6.045, which is the difference in average tip percent between smiley face and control groups. It also is the parameter estimate for \(b_1\). Try changing the b1 to b0 and run it again. This returns the estimate for \(b_0\), which in this case is the mean for the control group.
PRE
PRE is a second measure of effect size. As just discussed, it tells us the proportional reduction in error of a group model over the empty model. PRE is a nice measure of effect size because it is relative: it is a measure of improvement (reduction in error) that results from adding in the explanatory variable.
As with other statistics, PRE will vary from model to model and situation to situation. What level of PRE would count as a large effect, or meaningful effect, will vary as well across different research areas. This is something you will get a sense of as you gain more experience analyzing data and making models.
In the social sciences, at least, there are some generally agreed-on ideas about what is considered a strong effect. A PRE of .25 is considered a pretty large effect, .09 is considered medium, and .01 is considered small. Recall the Condition_model had a PRE of .07. According to these conventions, there is a small to medium effect of drawing smiley faces on tips. In contrast, the Height3Group model of thumb length had a PRE of .14, a medium to large effect size.
Take these conventions with a grain of salt, though, because effect size ultimately depends on your purpose. For example, if an online retailer found a small effect of changing the color of their “buy” button (e.g., PRE = .01), they might want to do it even though the effect is small. The change is free and easy to make and it might result in a tiny increase in sales.
R: The PRE() Function
Similar to the b1() function, the PRE() function will return the PRE for a model. In the code window below run supernova() on the Condition_model of tips. Look in the supernova table to see what the PRE is.
require(coursekata)
# run this code
Condition_model <- lm(Tip ~ Condition, data = TipExperiment)
supernova(Condition_model)
# run this code
Condition_model <- lm(Tip ~ Condition, data = TipExperiment)
PRE(Condition_model)
ex() %>%
check_function("PRE") %>%
check_result() %>%
check_equal()Now change the function supernova() to PRE() instead. It should return just the PRE, the same one you found in the complete ANOVA table. Later, when we introduce the concept of sampling distributions, you will see how useful these new functions, such as b1() and PRE(), can be.
Cohen’s d
A third measure of effect size that applies especially to two-group models (such as the condition model) is Cohen’s d. Cohen’s d indicates the size of a group difference in standard deviation units. For example, instead of saying smiley face tables tip 6 percent more than control tables, we could say that smiley tables’ tip percentages are 0.55 standard deviations greater than control tables.
Cohen’s d is related to the concept of z-score. Recall that z-scores tell us how far an individual score is from the mean of a distribution in standard deviation units. Both z-scores and Cohen’s d give us a way to judge the size of a difference regardless of the original units of measurement.
\[d=\frac{\bar{Y}_{1}-\bar{Y}_2}{s}\]
Calculating Cohen’s d: What Standard Deviation to Use?
If you try to calculate Cohen’s d, you will soon encounter a question: Which standard deviation should you use? The standard deviation of the outcome variable for the whole sample, or the standard deviation of the outcome variable within the two groups? If the group means are far apart, the standard deviation for the whole sample might be considerably larger than the standard deviation within each of the groups.
In general we will use the standard deviation within groups when calculating Cohen’s d, because this is our best estimate of the variation in outcome that is not accounted for by our model. But because the standard deviations will often differ from group to group, we need a way of combining two standard deviations into one.
One possibility is just to average the two standard deviations. This works fine if the two groups are the same size. But imagine a situation where the sample size in one group is 100, but in the other only 10. If we average the two standard deviations we are assigning the same importance to the estimate of standard deviation based on the group of 10 as to the estimate based on the group of 100, which doesn’t seem right. We should have more confidence in the estimate based on the larger sample.
The solution is to use a weighted average of the two standard deviations, weighted by the number of degrees of freedom in each group. This is often referred to as the “pooled standard deviation,” and this is what we use to calculate Cohen’s d. The pooled standard deviation is calculated like this:
\[s_{\text{pooled}}=\frac{\text{df}_1s_1+\text{df}_2s_2}{\text{df}_1+\text{df}_2}\]
Another way to find the pooled standard deviation is to simply take the square root of the Mean Square Error (or MS Error) in the ANOVA table. Mean Square Error, if you recall, is the Sum of Squares Error divided by the degrees of freedom for error, which yields a variance estimate based only on the variation within groups. In this case, the pooled standard deviation would be the square root of 121.64 (see table below), or about 11.
Analysis of Variance Table (Type III SS)
Model: Tip ~ Condition
SS df MS F PRE p
----- --------------- | -------- -- ------- ----- ------ -----
Model (error reduced) | 402.023 1 402.023 3.305 0.0729 .0762
Error (from model) | 5108.955 42 121.642
----- --------------- | -------- -- ------- ----- ------ -----
Total (empty model) | 5510.977 43 128.162 We can improve the formula for Cohen’s d by replacing \(s\) with \(s_{pooled}\):
\[d=\frac{\bar{Y}_{1}-\bar{Y}_2}{s_{pooled}}\]
R: The cohensD() function
As with everything else in this class, there is an R function for calculating Cohen’s d.
cohensD(Tip ~ Condition, data = TipExperiment) Try running this code in the code window.
require(coursekata)
# run this code
cohensD(Tip ~ Condition, data = TipExperiment)
cohensD(Tip ~ Condition, data = TipExperiment)
ex() %>% check_function("cohensD") %>% check_result() %>% check_equal()0.54813506569161We know that there is a tip percent difference of 6 between smiley face and control tables on average and the pooled standard deviation is about 11. Using standard deviation (11) as a unit of measurement, the mean difference between smiley face and control tables (6) is a little more than half a standard deviation (0.55 standard deviations, to be exact!).
With something like tipping, knowing there is about a 6 percentage point difference is actually pretty meaningful. But for other variables such as Kargle and Spargle scores, people may not be as clear what a straight point difference implies. Especially in these cases, reporting the difference in standard deviations (Cohen’s d) is quite useful.