Course Outline
-
segmentGetting Started (Don't Skip This Part)
-
segmentStatistics and Data Science: A Modeling Approach
-
segmentPART I: EXPLORING VARIATION
-
segmentChapter 1 - Welcome to Statistics: A Modeling Approach
-
segmentChapter 2 - Understanding Data
-
segmentChapter 3 - Examining Distributions
-
segmentChapter 4 - Explaining Variation
-
segmentPART II: MODELING VARIATION
-
segmentChapter 5 - A Simple Model
-
segmentChapter 6 - Quantifying Error
-
segmentChapter 7 - Adding an Explanatory Variable to the Model
-
7.5 Error Leftover From the Group Model
-
segmentChapter 8 - Digging Deeper into Group Models
-
segmentChapter 9 - Models with a Quantitative Explanatory Variable
-
segmentPART III: EVALUATING MODELS
-
segmentChapter 10 - The Logic of Inference
-
segmentChapter 11 - Model Comparison with F
-
segmentChapter 12 - Parameter Estimation and Confidence Intervals
-
segmentChapter 13 - What You Have Learned
-
segmentFinishing Up (Don't Skip This Part!)
-
segmentResources
list High School / Advanced Statistics and Data Science I (ABC)
7.5 Error Leftover From the Group Model
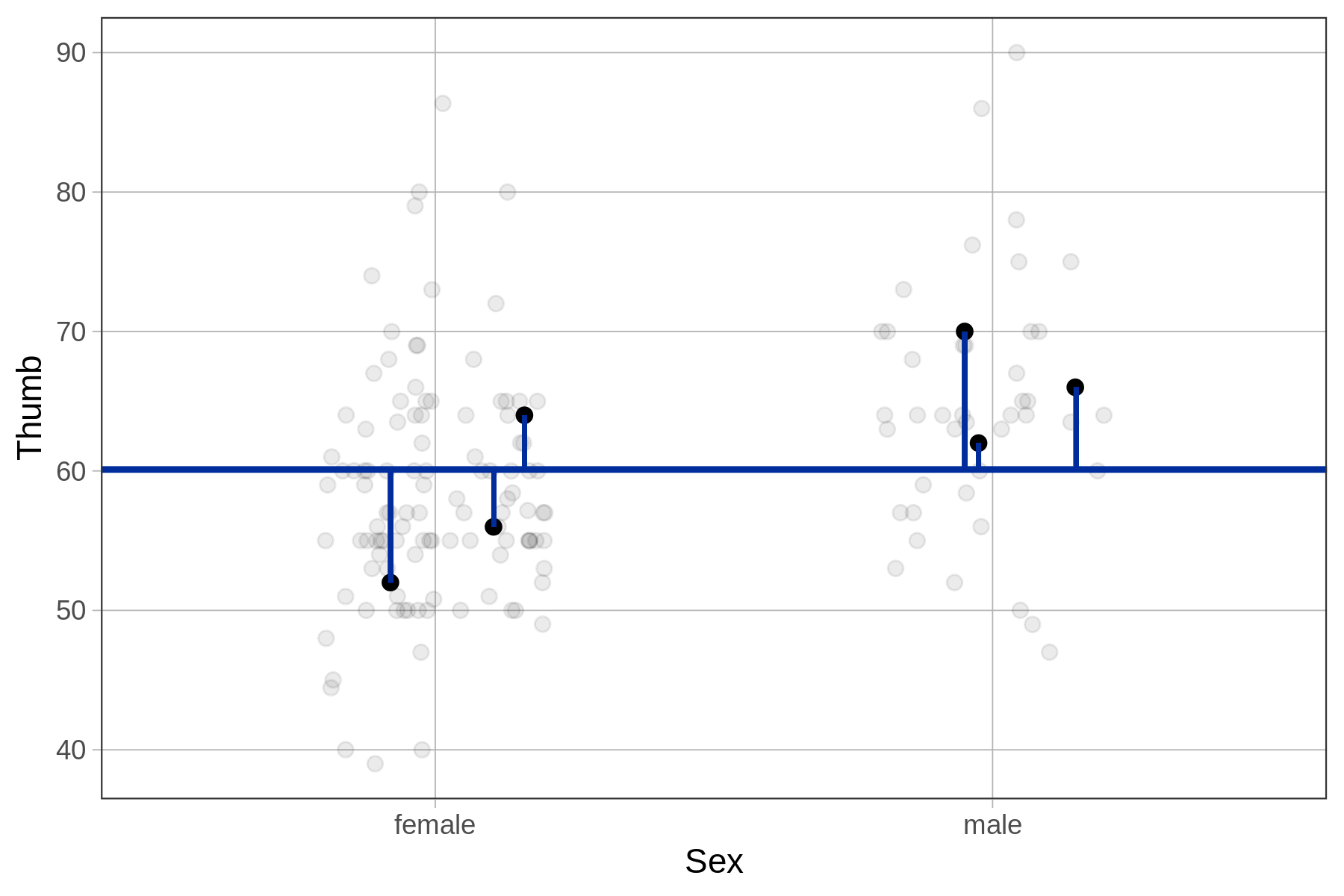
Previously, we calculated residuals from the empty model of Thumb by starting with the actual thumb length for each student, and then subtracting the predicted value based on the model. In the empty model, all students had the same predicted value.
DATA = MODEL PREDICTION + RESIDUAL
RESIDUAL = DATA - MODEL PREDICTION
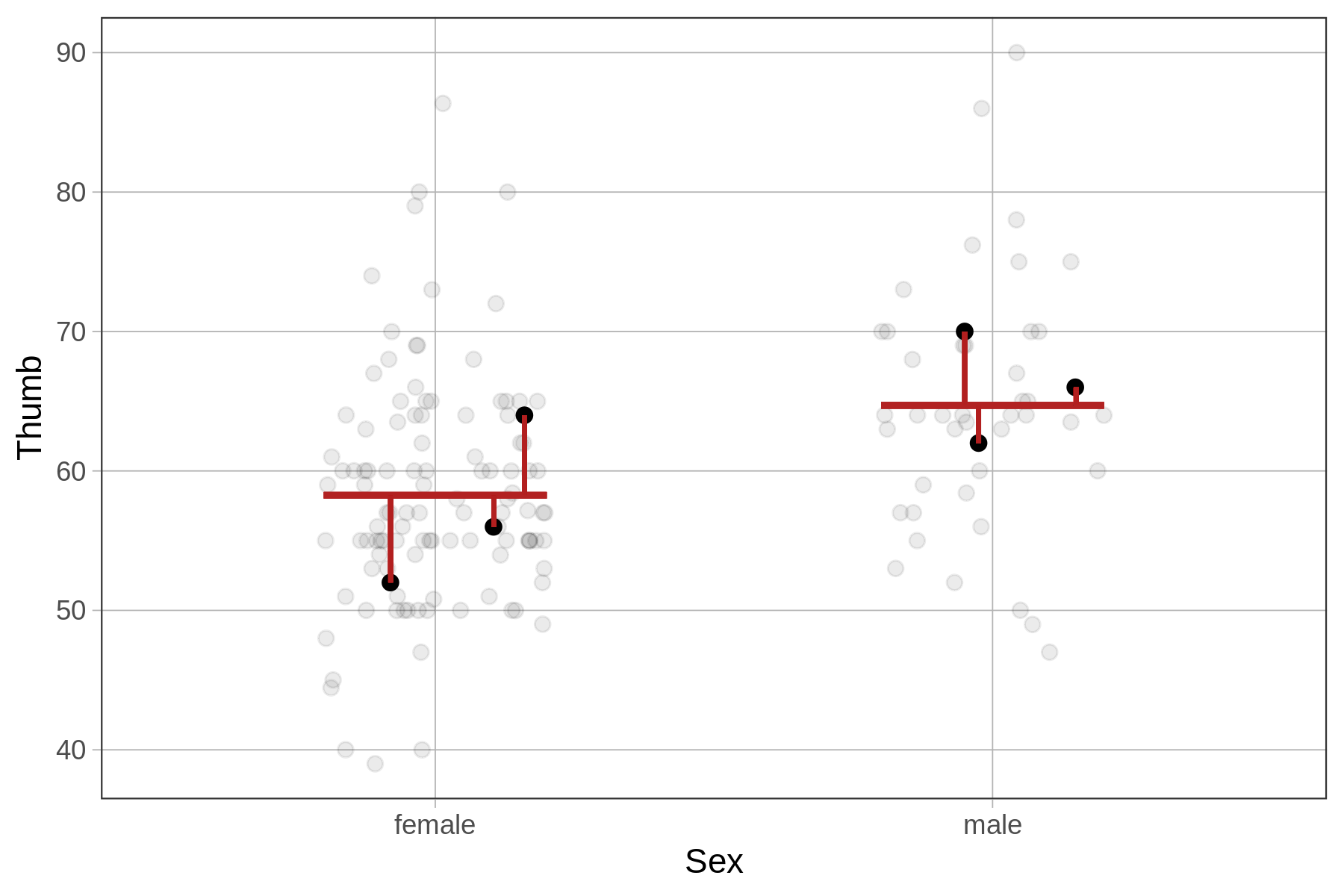
For the Sex model of Thumb we will use the same method, the only difference being that this time there will be two different model predictions, depending on the sex of the student. Still, the predicted thumb length for each student, which depends on their sex, is subtracted from their actual thumb length to get the residuals.
The residuals for 6 example students are represented in the plots below for both the empty model (left) and Sex model (right). Notice that the placement of the 6 data points is the same from one model to the other; the actual thumb lengths of these students don’t change.
| Residuals from the Empty Model | Residuals from the Sex Model |
|---|---|
|
|
|
The predictions and residuals of the two models, however, are different. For the empty model, each student’s residual is calculated in relation to the mean Thumb of all students in the data set. For the Sex model, each student’s residual is calculated in relation to the predicted Thumb for their sex.
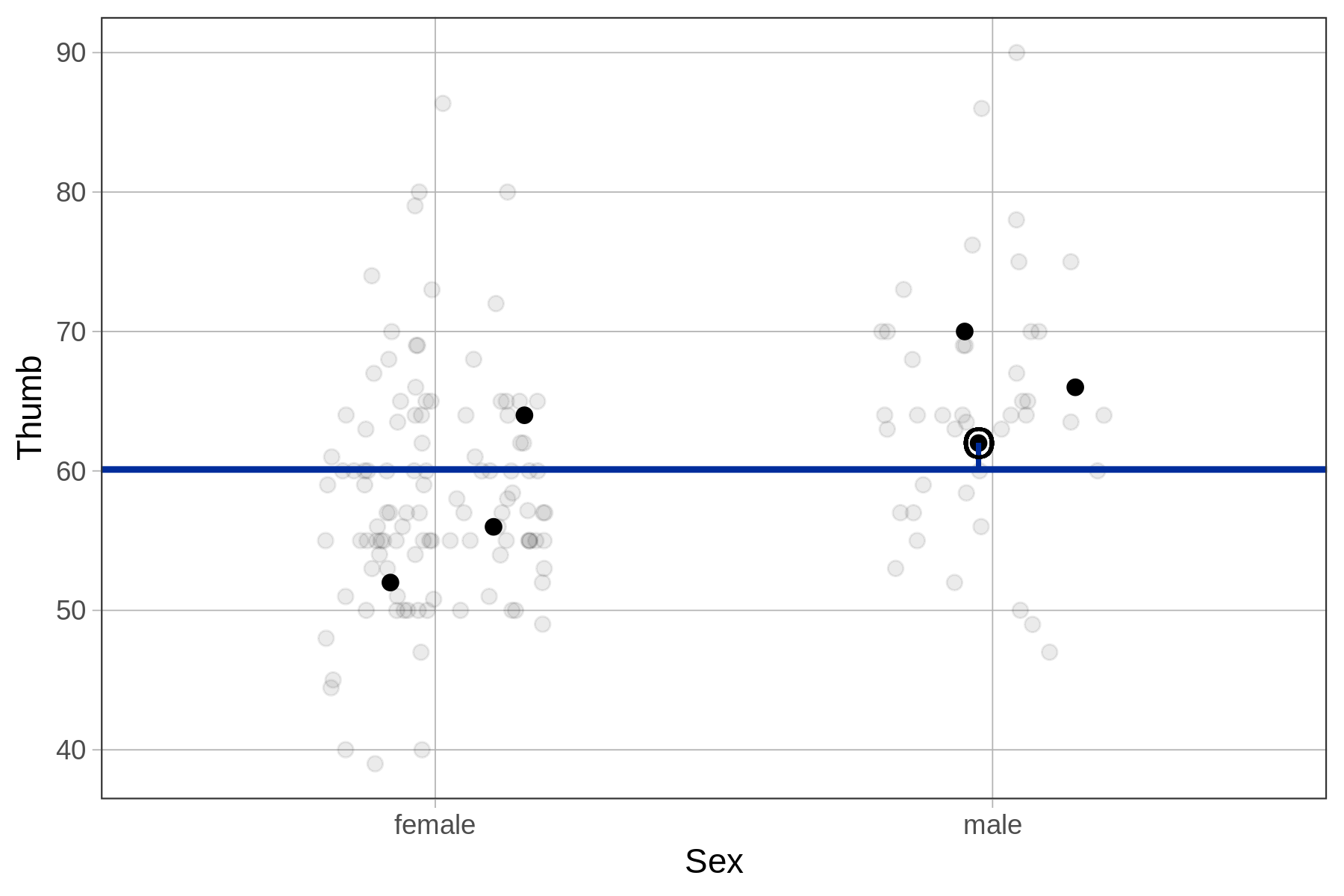
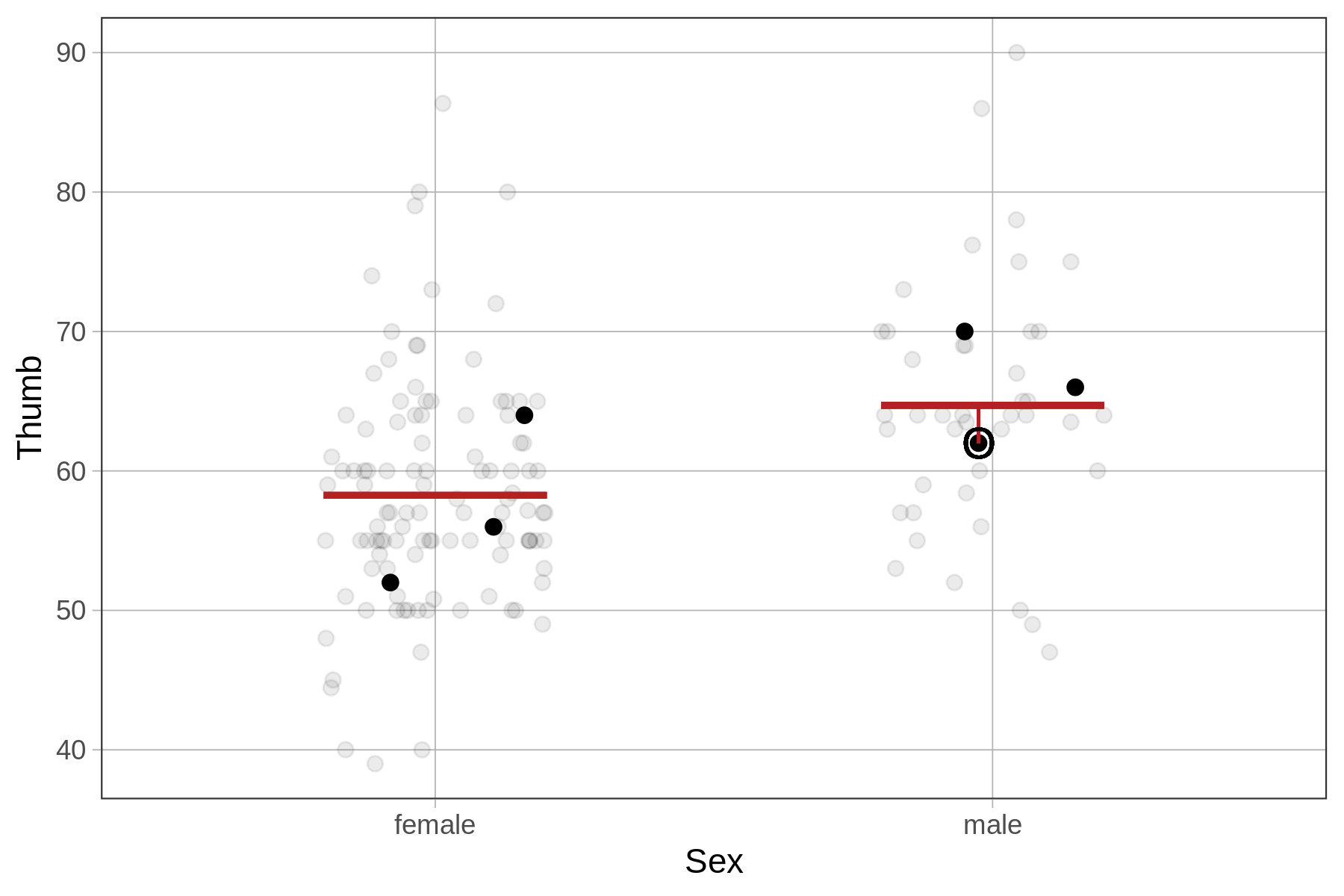
Something to keep in mind as well is that looking at residuals can help you interpret your data. Take, for example, the male student whose thumb length is circled in the plots below. Looking at residuals can help you see something interesting about this student.
| In relation to the empty model, this student has a larger than average thumb length. | In relation to the sex model, the same student has a slightly below average thumb length given that they are male. |
|---|---|
|
|
|
Using R to Calculate Residuals from the Sex Model
Just as we earlier used the predict() function to generate a predicted thumb length to each student in the data frame, we can use the resid() function to calculate the residual for each student. We’ve done that with the code below, and printed out the data table for just the 6 students we have been looking at.
Fingers$Sex_predict <- predict(Sex_model)
Fingers$Sex_resid <- resid(Sex_model)
head(select(Fingers, Sex, Thumb, Sex_predict, Sex_resid)) Sex Thumb Sex_predict Sex_resid
1 female 64 58.25585 5.744152
2 female 56 58.25585 -2.255848
3 female 52 58.25585 -6.255848
4 male 66 64.70267 1.297333
5 male 70 64.70267 5.297333
6 male 62 64.70267 -2.702667