Course Outline

list High School / Advanced Statistics and Data Science I (ABC)

Book
  • High School / Advanced Statistics and Data Science I (ABC)
  • High School / Statistics and Data Science I (AB)
  • High School / Statistics and Data Science II (XCD)
  • College / Statistics and Data Science (ABC)
  • College / Advanced Statistics and Data Science (ABCD)
  • College / Accelerated Statistics and Data Science (XCDCOLLEGE)
  • Skew the Script: Jupyter
  • CKHub: Jupyter made easy

9.8 Correlation

You might have heard of Pearson’s r, often referred to as a “correlation coefficient.” Correlation is just a special case of regression in which both the outcome and explanatory variables are transformed into z-scores prior to analysis.

Working with Standardized Variables

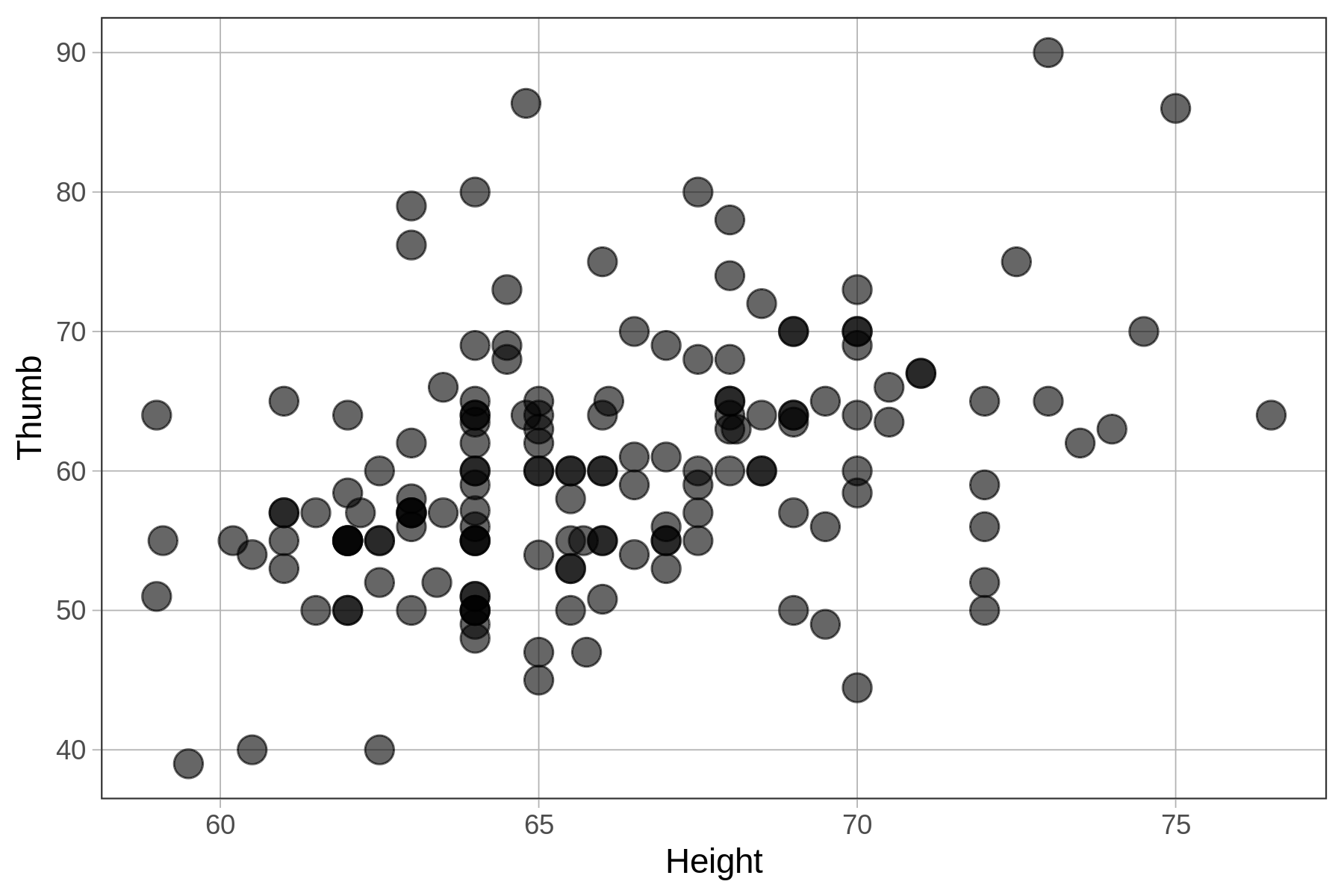
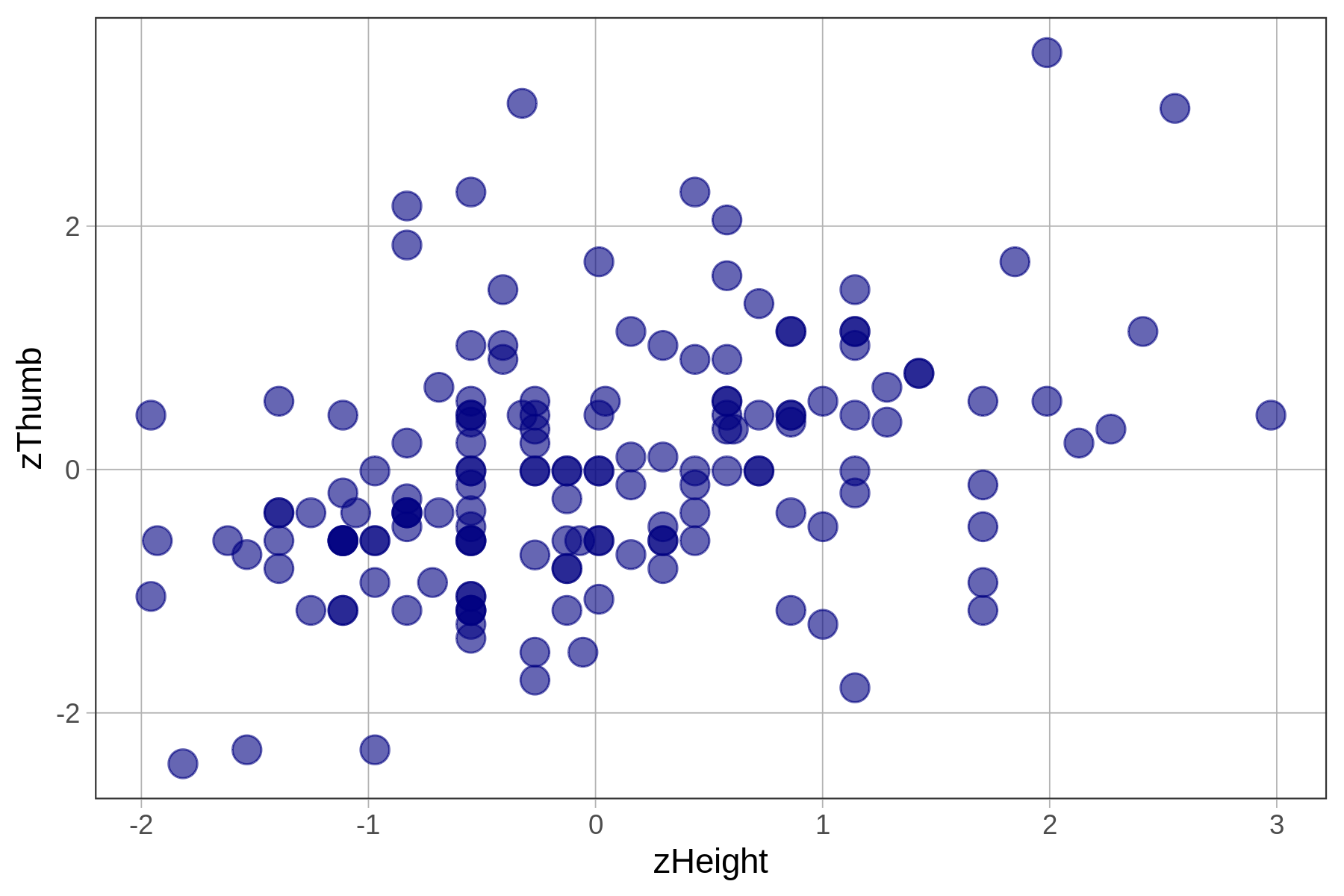
When we do a z-transformation on every value of a variable it is sometimes referred to as standardizing the variable. Let’s see what happens when we standardize the two variables we have been working with (Thumb and Height).

Use the code window below to create two new variables in the Fingers data frame: zThumb and zHeight. The function zscore() will standardize a variable by converting all of its values to z-scores.

require(coursekata) Fingers <- filter(Fingers, Thumb >= 33 & Thumb <= 100) # this transforms all Thumb lengths into z-scores Fingers$zThumb <- zscore(Fingers$Thumb) # modify this to do the same for Height Fingers$zHeight <- # this transforms all Thumb lengths into z-scores Fingers$zThumb <- zscore(Fingers$Thumb) # modify this to do the same for Height Fingers$zHeight <- zscore(Fingers$Height) ex() %>% check_object("Fingers") %>% { check_column(., "zThumb") %>% check_equal() check_column(., "zHeight") %>% check_equal() }
CK Code: B5_Code_Correlation_01

Because both variables are transformed into z-scores, the mean of each distribution will be 0, and the standard deviation will be 1.

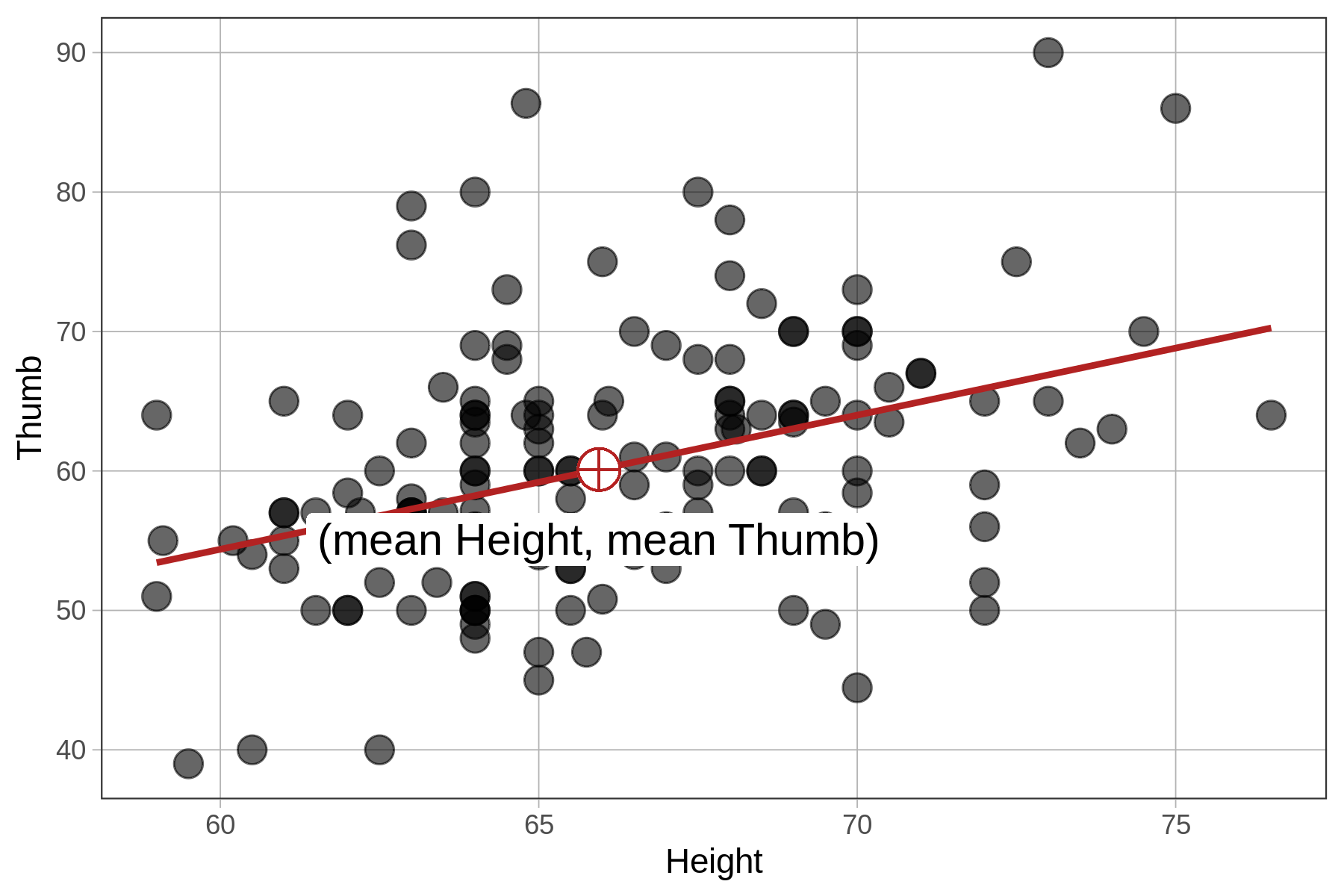
In this chapter we have been using height to explain the variation we see in thumb lengths. In the code window below, we have provided code to make a scatterplot of Thumb and Height. Modify the second line to make a scatterplot of zThumb by zHeight.

Make two scatterplots by modifying the code below.

require(coursekata) Fingers <- Fingers %>% filter(Thumb >= 33 & Thumb <= 100) %>% mutate( zThumb = zscore(Thumb), zHeight = zscore(Height) ) # this makes a scatterplot of the raw scores # size makes the points bigger or smaller gf_point(Thumb ~ Height, data = Fingers, size = 4) # zThumb and zHeight have already been created for you # modify the code below to make a scatterplot of the z-scores gf_point( , data = Fingers, size = 4, color = "navy") # this makes a scatterplot of the raw scores # size makes the points bigger or smaller gf_point(Thumb ~ Height, data = Fingers, size = 4) # zThumb and zHeight have already been created for you # modify the code below to make a scatterplot of the z-scores 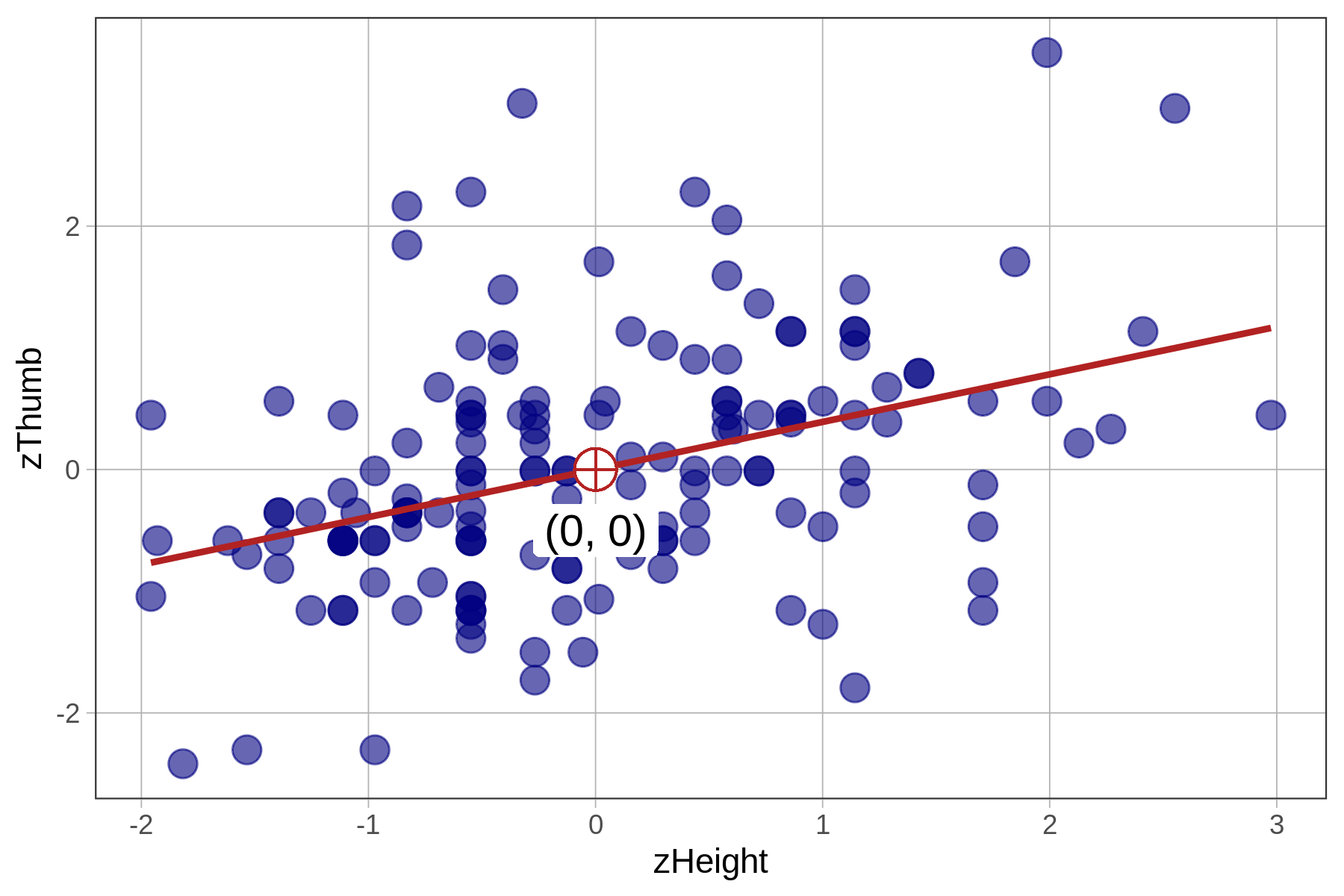gf_point(zThumb ~ zHeight, data = Fingers, size = 4, color = "navy") ex() %>% { check_function(., "gf_point", index = 1) %>% { check_arg(., "object") %>% check_equal() check_arg(., "data") %>% check_equal() } check_function(., "gf_point", index = 2) %>% { check_arg(., "object") %>% check_equal() check_arg(., "data") %>% check_equal() } }
CK Code: B5_Code_Correlation_02
Thumb ~ Height zThumb ~ zHeight

A scatterplot of the distribution of Thumb by Height.

A scatterplot of the distribution of zThumb by zHeight. The two distributions look the same except the scale of the axes.


Fitting the Regression Model to Standardized Variables

In the code window below we’ve provided the code to fit a regression line for Thumb based on Height. Add code to fit a regression model to the two transformed variables, predicting zThumb based on zHeight.

require(coursekata) Fingers <- Fingers %>% filter(Thumb >= 33 & Thumb <= 100) %>% mutate( zThumb = zscore(Thumb), zHeight = zscore(Height) ) Height_model <- lm(Thumb ~ Height, data = Fingers) # this fits a regression model of Thumb by Height lm(Thumb ~ Height, data = Fingers) # write code to fit a regression model predicting zThumb with zHeight # this fits a regression model of Thumb by Height lm(Thumb ~ Height, data = Fingers) # write code to fit a regression model predicting zThumb with zHeight lm(zThumb ~ zHeight, data = Fingers) ex() %>% check_function("lm", index = 2) %>% check_result() %>% 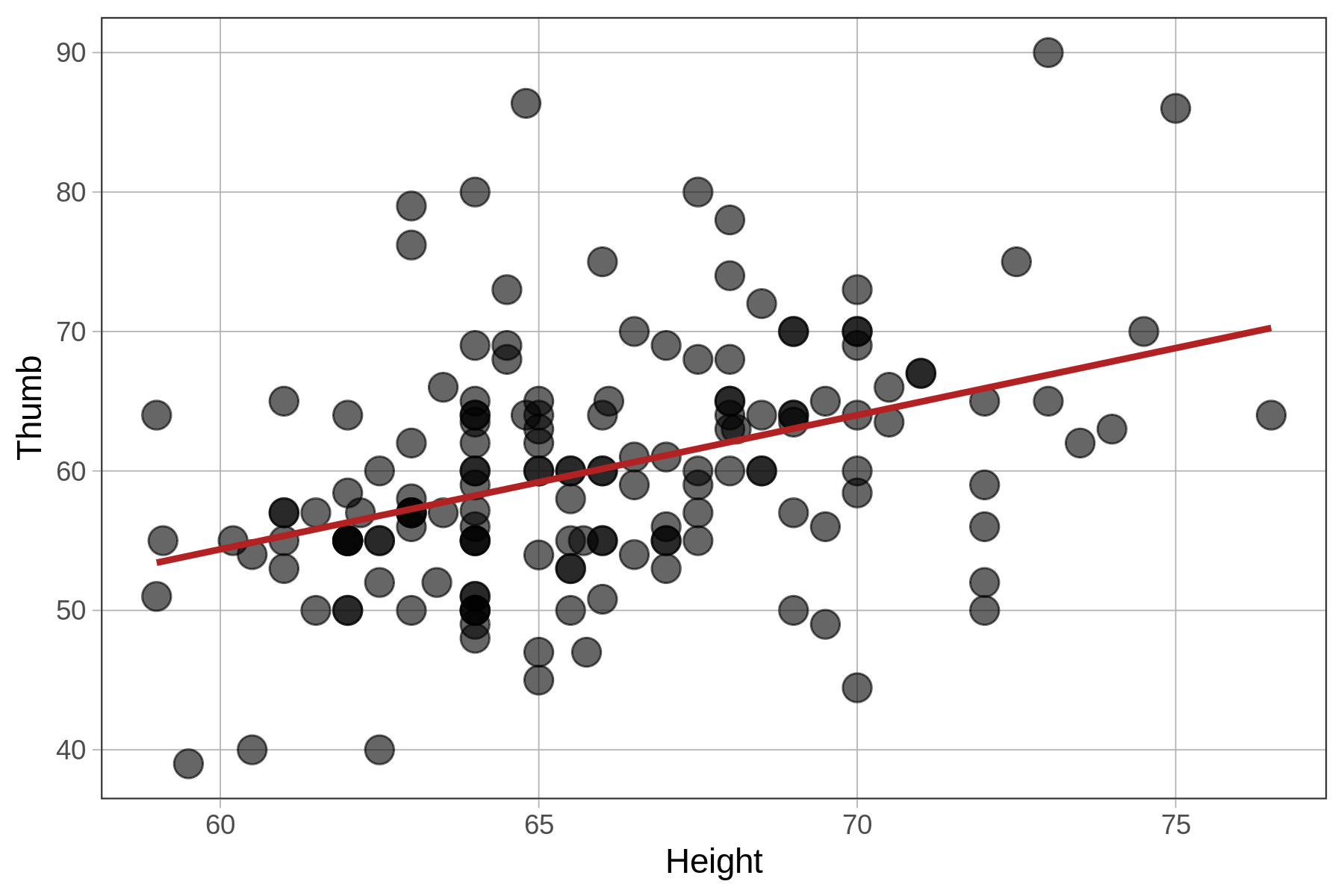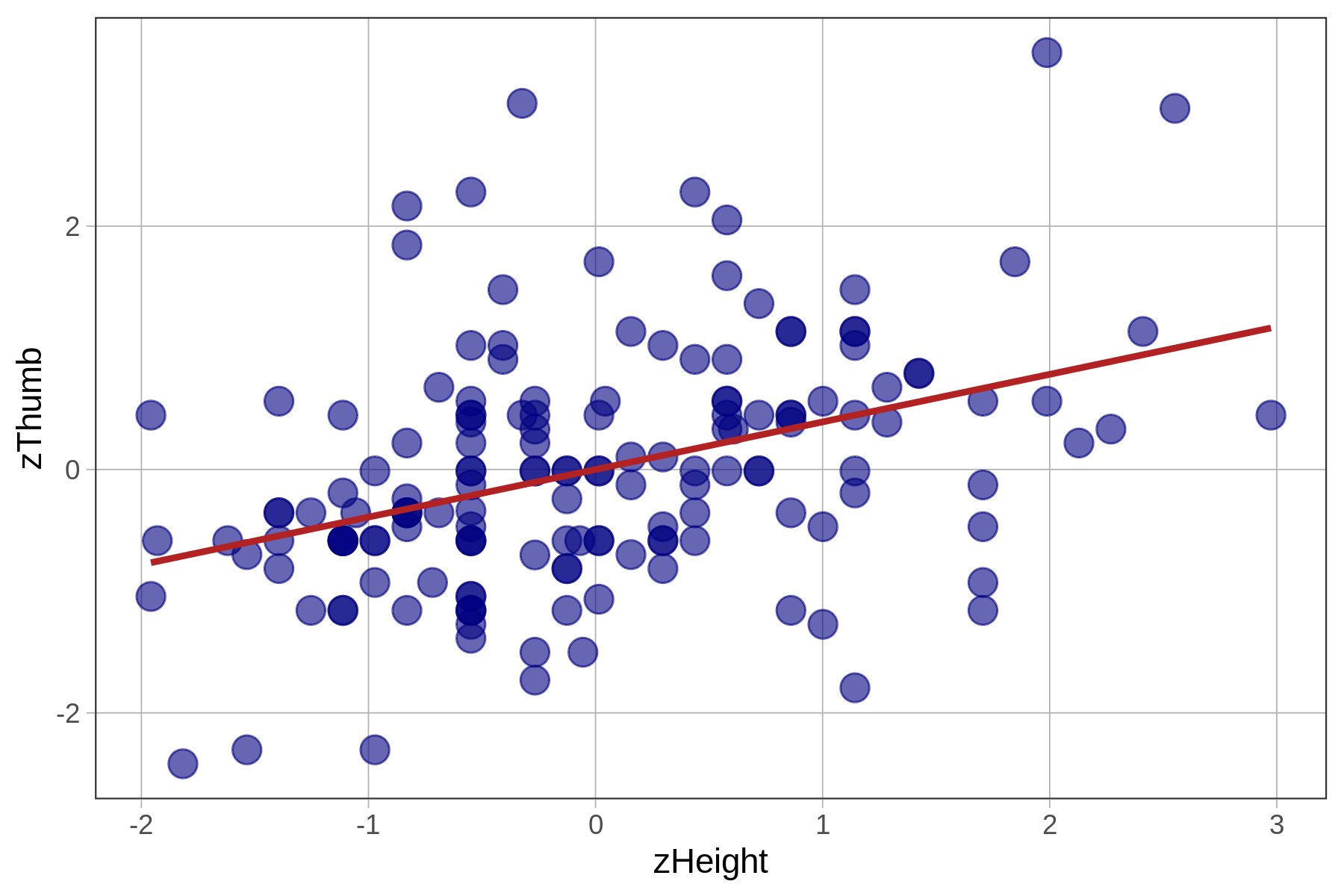check_equal()
CK Code: B5_Code_Correlation_03

In the table below we show the best-fitting parameter estimates along with the two scatterplots, this time with the best-fitting regression lines overlaid.

Thumb ~ Height zThumb ~ zHeight

A scatterplot of the distribution of Thumb by Height.

A scatterplot of the distribution of zThumb by zHeight. The two distributions look the same except the scale of the axes. 

Coefficients:
(Intercept)       Height  
    -3.3295       0.9619  
Coefficients:
(Intercept)      zHeight  
 -2.074e-16    3.911e-01


Note that R will sometimes express parameter estimates in scientific notation. Thus, -2.074e-16 means that the decimal point is shifted 16 digits to the left. So, the actual y-intercept of the best-fitting regression line is -.00000000000000018, which is, for all practical purposes, 0.

We know from earlier that the best-fitting regression line passes through the point of means, which is the point defined by the mean of both the outcome and explanatory variables, shown on the scatterplots below. Note that in the case of zThumb and zHeight, the mean of each is 0 and the point of means is (0,0).

\(\text{Thumb}_i = 3.33 + .96\text{Height}_i + e_i\) \(\text{zThumb}_i = .39\text{zHeight}_i + e_i\)

A scatterplot of the distribution of Thumb by Height overlaid with regression line. The point of means (mean height, mean thumb length) is shown on the regression line.

A scatterplot of the distribution of zThumb by zHeight overlaid with regression line. The point of means (0,0) is shown on the regression line.


Because the mean of any standardized variable is 0, a regression line based on standardized variables will always have a y-intercept of 0, meaning that when x is 0, y will also be 0.

Correlation coefficient: The slope of the standardized regression line

Let’s now turn our attention to the slopes (the \(b_1\) estimates) of both models, the one based on unstandardized variables and the one based on standardized variables.

Notice that the slopes are different for the unstandardized and standardized regression lines (.96 versus .39). To interpret the unstandardized slope, you need to know something about how thumbs and heights are measured (e.g., mm and inches). But the standardized slope does not require that additional knowledge.

The slope of the regression line between the standardized variables is called the correlation coefficient, or Pearson’s \(r\). The correlation coefficient is useful for assessing the strength of a bivariate relationship between two quantitative variables independent of the units on which each variable is measured.

To save you from having to transform variables into z-scores and then fit a regression line just to find out the correlation coefficient, R provides an easy way to directly calculate the correlation coefficient (Pearson’s \(r\)) from the raw scores: the cor() function. Try running the code in the window below.

require(coursekata) Fingers <- Fingers %>% filter(Thumb >= 33 & Thumb <= 100) %>% mutate( zThumb = zscore(Thumb), zHeight = zscore(Height) ) # this calculates the correlation of Thumb and Height cor(Thumb ~ Height, data = Fingers) cor(Thumb ~ Height, data = Fingers) ex() %>% check_function("cor") %>% check_result() %>% check_equal()
CK Code: B5_Code_Correlation_04
[1] 0.3910649

Notice that the result of .39 is, exactly, the slope of the standardized regression line, meaning that an increase of 1 standard deviation in height will result in a .39 standard deviation in thumb length.

Correlation coefficients, because they are calculated using standardized variables, have certain characteristics. The most useful of these is that \(r\) will always range from -1 to +1. An \(r\) of 0 means that the two variables are not related. A positive \(r\) means that the variables are positively and linearly related, while a negative \(r\) means they are negatively and linearly related.

A range of seven hypothetical scatterplot distributions appear arranged in a line from left to right. They display the expected distribution of points for various correlation coefficients, ranging from a correlation of positive one on the left, where all the points are arranged in a line that slopes upward, to a correlation of negative one on the right, where all the points are arranged in a line that slopes downward. The middle distribution is a scattered cloud of points and labeled as a correlation of zero. As the correlation gets further from zero, the points start to get closer to a line.

The further away from 0 \(r\) is, the stronger the linear relationship between the two variables. Two variables with a correlation of +1 are perfectly related, meaning that a 1 SD increase in one of the variables will produce a 1 SD increase in the other. A correlation of -1 means that two variables are perfectly negatively related.

Note that a relationship between two variables can be highly systematic, but not linear, for example, in the plots on the left and center below. In these cases, even though there is a clear pattern in the scatterplots, the \(r\) is close to 0 because the relationship is not linear.

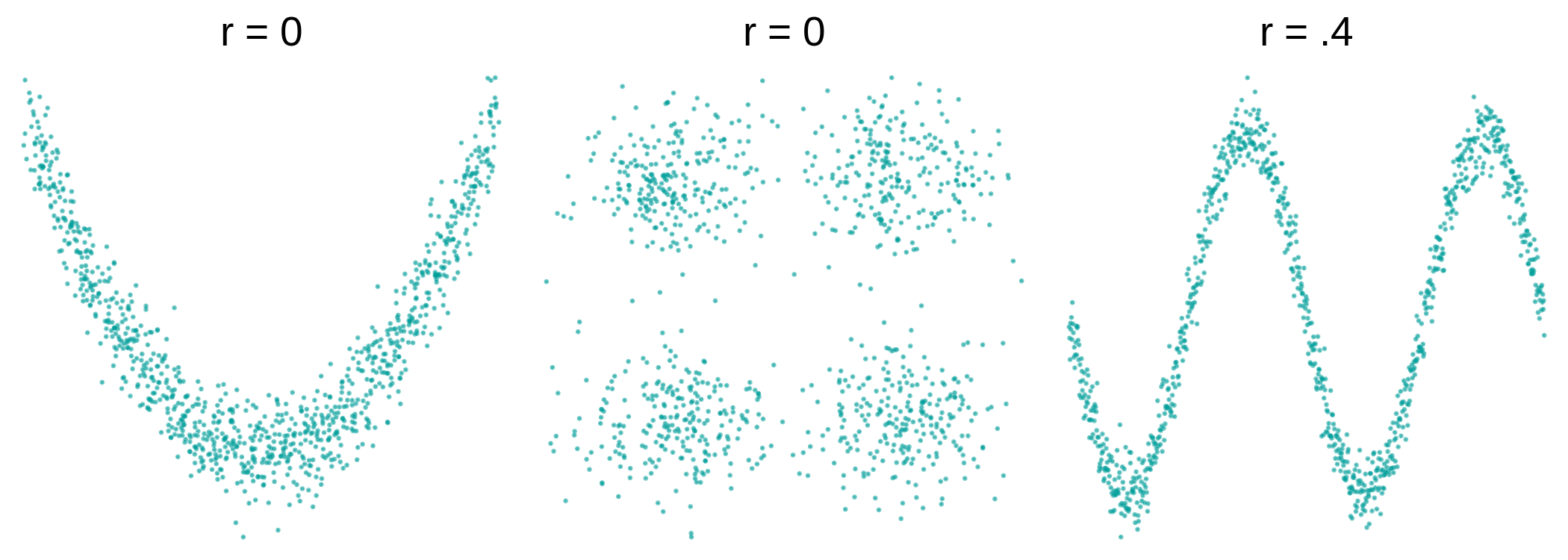
Three side-by-side hypothetical scatterplot distributions. Each distribution has a distinct shape and pattern, but none of them are a linear pattern. The first one appears to curve like a parabola and has a correlation of zero. The second one appears to have four unique quadrants where the points tend to be clumped together and has a correlation of zero. The third one appears to curve up and down in a wave pattern and has a correlation of point four.

Even when the \(r\) isn’t necessarily close to 0, as in the plot on the right where the \(r = .4\), it doesn’t mean that a straight regression line is the best model for it (perhaps a curved one will be better).

Responses

Responses
close