Course Outline

list High School / Advanced Statistics and Data Science I (ABC)

Book
  • High School / Advanced Statistics and Data Science I (ABC)
  • High School / Statistics and Data Science I (AB)
  • High School / Statistics and Data Science II (XCD)
  • High School / Algebra + Data Science (G)
  • College / Introductory Statistics with R (ABC)
  • College / Advanced Statistics with R (ABCD)
  • College / Accelerated Statistics with R (XCD)
  • CKHub: Jupyter made easy

12.7 Using the t-Distribution to Construct a Confidence Interval

Just as we used the t-distribution in the previous chapter to model the sampling distribution of \(b_1\) for purposes of calculating a p-value (the approach used by supernova()), we can use it here to calculate a 95% confidence interval.

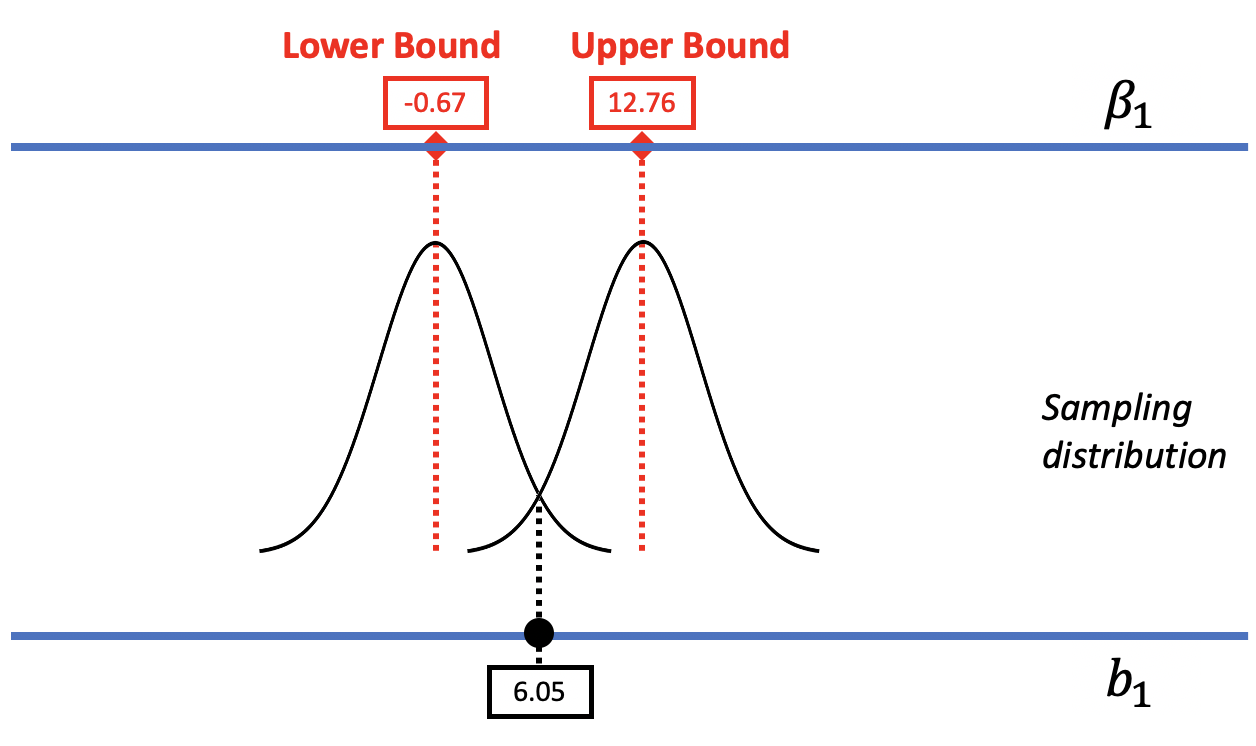
In the figure below, we replaced the resampled sampling distribution of \(b_1\)s with one modeled by the smooth t-distribution with its associated standard error. As before, we can mentally move the t-distribution down and up the scale to find the lower and upper bounds of the confidence interval.

A three-layered diagram of beta-sub-1, the sampling distribution of b1, and the sample b1, wherein, there are two outlines of potential sampling distributions. Their tails are overlapping. The one on the left represents a possible DGP where the sampling distribution is centered at 6.05, and the sample b1 of 6.05 falls right in the center as well. The outline on the right represents a possible DGP where beta-sub-equals 12.76, so the sampling distribution is also centered at 12.76. The sample b1 of 6.05 falls right on the line for the boundary of the lower tail for this distribution. In the top line, the beta-sub-1 of negative 0.67 is labeled as the Lower Bound, and the beta-sub-1 of 12.76 is labeled as the Upper Bound. We can also see that where the upper tail of the left outline and the lower tail of the right outline intersect, that is where the sample b1 of 6.05 lies.

The R function that calculates a confidence interval based on the t-distribution is confint().

Here’s the code you can use to directly calculate a 95% confidence interval that uses the t-distribution as a model of the sampling distribution of \(b_1\):

confint(lm(Tip ~ Condition, data = TipExperiment))

The confint() function takes as its argument a model, which results from running the lm() function. In this case we simply wrapped the confint() function around the lm() code. You could accomplish the same goal using two lines of code, the first to create the model, and the second to run confint(). Try it in the code block below.

require(coursekata) # create the condition model of tip and save it as Condition_model Condition_model <- confint(Condition_model) # create the condition model of tip and save it as Condition_model Condition_model <- lm(Tip ~ Condition, data = TipExperiment) confint(Condition_model) ex() %>% check_function("lm") %>% check_result() %>% check_equal()
                         2.5 %   97.5 %
(Intercept)          22.254644 31.74536
ConditionSmiley Face -0.665492 12.75640

As you can see, the confint() function returns the 95% confidence interval for the two parameters we are estimating in the Condition model. The first one, labelled Intercept, is the confidence interval for \(\beta_0\), which we remind you is the mean for the Control group. The second line shows us what we want here, which is the confidence interval for \(\beta_1\).

Using this method, the 95% confidence interval for \(\beta_1\) is from -0.67 to 12.76. Let’s compare this confidence interval to the one we calculated above on the previous page using bootstrapping: 0 to 13. While these two confidence intervals aren’t exactly the same, they are darn close, which gives us a lot of confidence. Even when we use very different methods for constructing the confidence interval, we get very similar results.

Margin of Error

One way to report a confidence interval is to simply say that it goes, for example, from -0.67 to 12.76. But another common way of saying the same thing is to report the best estimate (6.05) plus or minus the margin of error (6.72), which you could write like this: \(6.05 \pm 6.72\).

A diagram of beta-sub-1 and the margin of error depicted as a horizontal line. It shows the distance between the best estimate of beta-sub-1, of 6.05, to the lower bound point of negative 0.67 is a distance of negative 6.72. And the distance between the best estimate of beta-sub-1, of 6.05, to the upper bound point of 12.76 is a distance of 6.72.

The margin of error is the distance between the upper bound and the sample estimate. In the case of the tipping experiment this would be \(12.76 - 6.05\), or $6.72. If we assume that the sampling distribution is symmetrical, the margin of error will be the same below the parameter estimate as it is above.

We can always calculate the margin of error by using confint() to get the upper bound of the confidence interval and then subtracting the sample estimate. But we can do a rough calculation of margin of error using the empirical rule. According to the empirical rule, 95% of all observations under a normal curve fall within plus or minus 2 standard deviations from the mean.

Applying this rule to the sampling distribution, the picture below shows that the margin of error is approximately equal to two standard errors. If we start with a t-distribution centered at the sample \(b_1\), we would need to slide it up about two standard errors to reach the cutoff above which \(b_1\) (6.05) falls into the lower .025 tail.

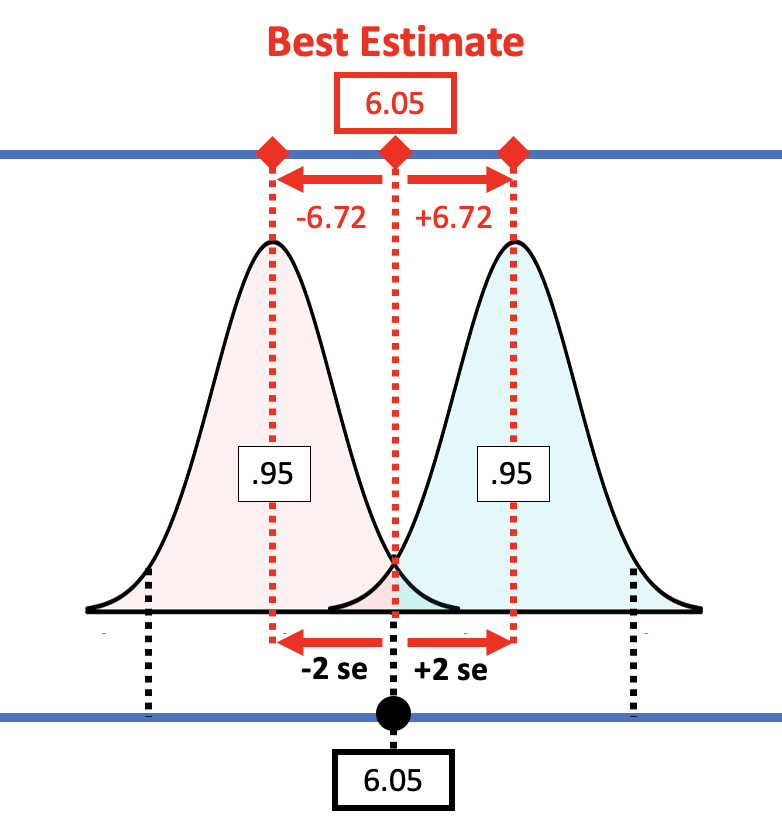
A diagram that shows the distance of negative 6.72 between the best estimate of 6.05 and the lower bound of negative 0.67 is also a distance of about 2 negative standard errors, and the distance of 6.72 between the best estimate of 6.05 and the upper bound of 12.76 is also a distance of about 2 standard errors.

If you have an estimate of standard error, you can simply double it to get the approximate margin of error. If, for example, we use the standard error generated by R (3.33) for the condition model, the margin of error would be twice that, or 6.66. That’s pretty close to the margin of error we calculated from confint(): 6.72.

R uses the Central Limit Theorem to estimate standard error, but we also have other ways of getting the standard error. Using shuffle() to create the sampling distribution resulted in a slightly larger standard error of 3.5. If we double that, we get a margin of error of 7, slightly larger than the 6.66 we got using R’s estimate of standard error. In general, if the standard error is larger, the margin of error will be larger and so will the confidence interval.

Responses

Responses
close